[模拟]来一瓶82年拉菲（酒杯问题）

问题描述：

悠神最近过生日，朋友纷纷来贺。现有一瓶82年拉菲与若干酒杯。酒杯呈三角形酒塔摆放，即每一个酒杯摆放在下一层两个酒杯中间，最下面一层酒杯摆放在桌面上。共有N(1<=N<=20)层酒杯，第k层共有k个酒杯。悠神将拉菲倒进第一层的酒杯中，速度为1杯/s，倒满后酒会向左右两个方向溢出，假设会全部溢出到这个酒杯下面相邻的两个酒杯中。然而悠神有洁癖，他不喜欢浪费，更不喜欢浸湿他心爱的桌布，所以请你计算一下第几秒之后桌布会被浸湿。

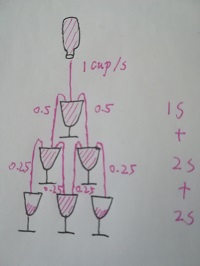
eg：如图所示为3层时的情况。第一层倒满需要1s，第二次倒满需要2s，第三层首次倒满需要2s。所以共需1+2+2=5s。

输入：

输入N(1<=N<=20)。

输出：

桌布浸湿时至少所需时间（取整数）。

输入样例：

输出样例：

分析：

桌布浸湿只与最下层最中间位置何时倒满有关，因此只需计算最下层中间位置酒杯的状态。由于时间取整，所以只需模拟出第一杯共倒了多少杯酒，即为多少s。而每一个酒杯共倒了多少酒与上一层相邻两个酒杯相关，及第i层第j个酒杯的酒只与第i-1层第j-1个和第j个酒杯的酒相关。及wine[i][j]=wine[i-1][j-1]+wine[i-1][j];由于酒杯有两种状态，及未满状态和倒满状态，所以要判断wine[i-1]层的酒是否>1。

#include<stdio.h>  
#include<string.h>  
#define MAXN 20  
int main() {  
    int N;  
    while (~scanf("%d", &N)) {  
        double wine[MAXN + 1][MAXN + 1] = { 0 };  
        double temp = 0;  
        while (wine[N][N / 2 + 1] < 1) {  
            memset(wine, 0, sizeof(wine));  
            temp++;  
            wine[1][1] = temp;  
            for (int i = 1; i <= N; i++) {  
                for (int j = 1; j <= i; j++) {  
                    wine[i][j] += (wine[i - 1][j - 1] > 1 ? (wine[i - 1][j - 1] - 1) / 2.0 : 0) + (wine[i - 1][j] > 1 ? (wine[i - 1][j] - 1) / 2.0 : 0);  
                }  
            }  
        }  
        printf("%g\n", wine[1][1]);  
    }  
    return 0;  
}