ccpc-wannafly秦皇岛站集训部分题解

发表于 | 分类于 ， | 热度 ℃
字数统计: 6,480 | 阅读时长 ≈ 29

WANNAFLY_DAY1

Problem A. Birthday

恬恬的生日临近了。宇扬给她准备了一个大蛋糕。

正如往常一样，宇扬在蛋糕上插了n支蜡烛，并把蛋糕分为m个区域。因为某种原因，他必须把第i根蜡烛插在第ai个区域或第bi个区域。区域之间是不相交的。宇扬在一个区域内同时摆放x支蜡烛就要花费x2的时间。宇扬布置蛋糕所用的总时间是他在每个区域花的时间的和。

宇扬想快些见到恬恬，你能告诉他布置蛋糕最少需要多少时间吗？

Input

第一行包含两个整数n，m（1 ≤ n ≤ 50， 2 ≤ m ≤ 50）。
接下来n行，每行两个整数ai, bi（1 ≤ ai, bi ≤ m）。

Output

一个整数表示答案

Examples

standard input
3 3
1 2
1 2
1 2

standard output

5

standard input

3 3
1 2
2 3
1 3

standard output

3

思路：

考虑费用流时把每个part拆成n个点，选择第i个点的代表为放置i块蛋糕和(i - 1)块蛋糕的时间差，这个时间差是增的，因此在费用流的过程中必定会从小到大选择
具体建图：左边n个点代表n个蛋糕，右边m * n个点代表m个part,每个part拆成n个点。源点向每个左边的点连一条流量1费用0的边，每个右边的点向汇点连一条流量1费用0的编。每个蛋糕向可以放的两个part的所有点连边，连向第i个点的费用为i^2 - (i - 1)^2，流量为1。这样求最小费用流既为答案。

Problem B. Board

恬恬有一个n × n的数组。她在用这个数组玩游戏：

开始时，数组中每一个元素都是0。

恬恬会做某些操作。在一次操作中，她可以将某一行的所有元素同时加上一个值，也可以将某一列的所有元素同时加上一个值。

在几次操作后，一个元素被隐藏了。你能帮助她回忆隐藏的数是几吗？

Input

第一行一个整数n（1 ≤ n ≤ 1000）。
接下来n行每行n个整数表示数组a。
第(i + 1)行的第j个元素表示aij（aij = −1或0 ≤ aij ≤ 100000）。−1表示隐藏的元素

Output

仅一个整数表示答案

Example

standard input
3
1 2 1
0 -1 0
0 1 0

standard output

1

思路

把格子N染色，第i行第j列格子的颜色为(i + j) % N。那么每次操作时，必定是N种不同的颜色都有一格被操作到，因此最后任何颜色格子的和必定是相等的。因此只需要记录每种颜色格子的和，并算出缺失格子的颜色C，用其余颜色的和减去颜色C的和即可

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn = 1005;
int map[maxn][maxn];
int main()
{
	int n;
	int x,y;
	while(cin>>n)
	{
		for(int i=0;i<n;i++)
		{
			for(int j=0;j<n;j++)
			{
				cin>>map[i][j];
				if(map[i][j]==-1) 
				{
					x=i;
					y=j;	
				}	
			}
		}
		
		for(int i=0;i<n;i++)
		{
			if(i==x) continue;
			int minn=0x3f3f3f;
			for(int j=0;j<n;j++)
			{
				minn=min(minn,map[i][j]);
			}
			for(int j=0;j<n;j++)
			{
				map[i][j]-=minn;
			}	
		}
		for(int i=0;i<n;i++)
		{
			if(i==y) continue;
			int minn=0x3f3f3f;
			for(int j=0;j<n;j++)
			{
				minn=min(minn,map[j][i]);
			}
			for(int j=0;j<n;j++)
			{
				map[j][i]-=minn;
			}
		}
		int ans1=0,ans2=0;
		for(int i=0;i<n;i++)
		{
			if(map[i][y]!=0 && map[i][y]!=-1) ans1=map[i][y];
		}
		for(int i=0;i<n;i++)
		{
			if(map[x][i]!=0 && map[x][i]!=-1) ans2=map[x][i];
		}
		cout<<ans1+ans2<<endl;
	}
	return 0;
}

Problem C. Circle

现在我们要把1 . . . n这n个数字首尾连接组成一个环，使得相邻元素互质的对数尽可能多。请输出最大对数。

Input

一行一个整数n(1 ≤ n ≤ 1000)。

Output

一行一个整数表示答案。

Example

standard input

4

standard output
4

Note

样例的一种构造方法为1 4 3 2。

思路

因为(i,i+1)=1且(1,n)=1，所以把1…n依次放进一个环，就可以啦。答案为n。

代码

1
2
3
4
5
6
7
8
9
10
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+7;
int main(){
	int t;
	while(cin>>t){
	cout<<t<<endl;	
	}
	return 0;
}

Problem D. 土龙弟弟

Problem E. Growth

弱弱有两个属性a和b，这两个属性初始的时候均为0，每一天他可以通过努力，让a涨1点或b涨1点。

为了激励弱弱努力学习，我们共有n种奖励，第i种奖励有xi，yi，zi三种属性，若a ≥ xi且b ≥ yi，则弱
弱在接下来的每一天都可以得到zi的分数。

问m天以后弱弱最多能得到多少分数。

Input

第一行一个两个整数n和m（1 ≤ n ≤ 1000，1 ≤ m ≤ 2000000000）。
接下来n行，每行三个整数xi，yi，zi（1 ≤ xi, yi ≤ 1000000000，1 ≤ zi ≤ 1000000）。

Output

一行一个整数表示答案。

Example

standard input
2 4
2 1 10
1 2 20

standard output

50

Note

在样例中，弱弱可以这样规划：第一天a涨1，第二天b涨1，第三天b涨1，第四天a涨1。
共获得0 + 0 + 20 + 30 = 50分

思路

把奖励的x拿出来从小到大排序，得到x1,x2,…,xn。
把奖励的y拿出来从小到大排序，得到y1,y2,…,yn。
用v[i][j]表示a值到达xi，b值达到yi时接下来每天可以得到的奖励。
v[i][j] = v[i - 1][j] + v[i][j - 1] - v[i - 1][j - 1] + t[i][j]
其中t[i][j]为满足x=i，y=j的奖励的总和。
用f[i][j]表示a值达到xi，b值达到yj时已经拿到的奖励的最大值。
f[i][j] + (x[i + 1] - x[i] - 1) t[i][j] + t[i + 1][j] -> f[i + 1][j]
f[i][j] + (y[j + 1] - y[j] - 1) t[i][j] + t[i][j + 1] -> f[i][j + 1]
最后统计一下答案就可以了。

Problem F. Kingdom

X王国有n位官员，编号从1到n。国王是1号官员。除了国王以外，每个官员都有一个上司。我们称这个
官员是这个上司的下属。上司的编号总比下属小。

我们定义一个官员的影响力为他所有下属的影响力之和再加1。例如，一个没有下属的官员的影响力
是1。国王的影响力总是n。

任何一位有下属的官员总是选择他的下属中影响力最高的作为他的心腹（有若干下属影响力相同的话则
会选择编号最小的）。

一位官员得到一条消息后，他就要把消息传达给国王。我们定义一位官员的花费为他将消息传达给国王
的花费。国王自己的花费为0。如果一位官员是他上司的心腹，则他的花费等于他上司的花费，否则他
的花费为他上司的花费加1。

由于时代和平，消息并不需要传递的太快。我们希望你决定每位官员（除了国王）的上司，使得所有官
员的花费之和和尽量小。

Input

一个整数n（1 ≤ n ≤ 8000）表示包括国王在内的官员的总数。

Output

一个整数表示最大的花费之和。

Example

standard input
4

standard output

2

思路

f[i]代表i个点时的答案，g[i][j]代表若干颗树加起来，size和为i，每棵树size<=j时，这些树的代价和最大是多少
从1到n枚举i，在i固定时枚举心腹的影响力大小更新f[i]，然后用类似背包的思路更新g[i][1]~g[i][i]
复杂度O(N^2)

Problem G. Matrix

弱弱有一个n × m的矩阵，第i行第j列位置上的值为aij。
弱弱定义以(x, y)为顶点，大小为k的三角形为：

第x行y位置，
第x + 1行y − 1，y，y + 1位置，
. . .，
第x + k − 1行y − k + 1，. . .，y + k − 1位置组成的区域。

比如说，以(1, 3)为顶点，大小为3的三角形为

OOXOOOO
OXXXOOO
XXXXXOO
OOOOOOO
中打叉的位置。

现在弱弱想要知道所有大小为k的三角形中，重心位置离顶点最近的是哪个？重心是三角形中每个位置
按照它们的值加权平均所得的点。
请输出这个最小距离（欧几里得距离）。

Input

第一行一个三个整数n，m，k（1 ≤ n ≤ 1000，1 ≤ m ≤ 1000，1 ≤ k ≤ min n,(m + 1)/2

接下来n行，每行m个整数aij（1 ≤ aij ≤ 1000）表示每个位置的重量。

Output

一行一个数表示答案。相对误差或绝对误差在10−5（1e-5）之内均会被判断为正确。

Example

standard input
2 3 2
1 1 1
1 1 1

standard output

0.7500000000

Note

只有一个大小为2的三角形。

思路

w个格子的重心的坐标为（∑xiwi / ∑wi, ∑yiwi / ∑wi)。
那么其实我们只要维护∑xiwi，∑yiwi，∑wi就可以了。
假设我们现在有一个顶点为(x, y)的三角形，我们想要推到顶点为(x, y+1)的三角形，观察两者之间的差异，会发现在推过去的过程中，其实就是删去了一个斜条，又加入了一个斜条。
同理，从(x, y)到(x+1, y)其实只是删去了两个斜条，加上了底上的横条，而这些关键的值都是可以通过前缀和的方法维护。

Problem H. Mountain

平面上有n座山，每座山都有左右两面，第i座山的高度为ai，现在弱弱在第一座山的左边山脚下（高度为0），他想要依此爬过这些山，到达第n座山的右边山脚下。

除了简单的爬上爬下，还有一种特殊操作。

如果弱弱目前在第i座山右面的海拔x的位置，且第j(i < j)座山的海拔大于等于x，且第i + 1, . . . , j − 1座山中没有一座山的海拔高于x，那么他可以使用绳索滑到第j座山左面海拔x的位置。

弱弱想找到一种方式，使得他在行程中海拔变化的幅度最小。请输出最小幅度。

Input

第一行一个整数n（1 ≤ n ≤ 1000）。
接下来一行n个整数ai（1 ≤ ai ≤ 1000）表示每座山的高度。

Output

一行一个整数表示答案。

Example

standard input
5
1 3 5 4 2

standard output

10

思路

考虑山中最高的一座，最优操作一定是从第一座山的左下角开始不停地往上爬，然后从最高的山不停地往下爬爬到最后一座山的右下角。
所以答案为最高山的高度*2。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<bits/stdc++.h>
using namespace std;
int a[1007], n;
int main(){
 while(cin>>n){
  int cnt = 0;
  a[0] = 0;
  int cur = 0;
  for(int i = 1;i<=n;i++){
   cin>>a[i];
   if(a[i] >= a[cur]){
    cnt += abs(a[i] - a[cur]);
    cur = i;
   }
  }
  while(cur<n){
   int cur2 = cur+1;
   for(int i = cur2;i<=n;i++){
    if(a[i] >= a[cur2]){
     cur2 = i;
    }
   }
   cnt+=abs(a[cur2]-a[cur]);
   cur = cur2;
  }
  cnt+=a[n];
  cout<<cnt<<endl;
 }
 return 0;
}

Problem I. 清明梦超能力者黄

黄YY是一个清明梦超能力者，同时也是一个记忆大师。他能够轻松控制自己在梦中的一切，在醒来之
后还能清晰的记得梦中所有的细节，这让他的朋友们都十分羡慕。

又是一个晚上，黄YY又到了自己的梦中，并且随手造出了一棵有n个点的树，树上每个点有一个初始颜
色0。为了让这棵树不那么单调，黄YY拿起了画笔在上面尽情上色。每一次上色可以用u, v, c来描述，代
表黄YY把u, v这条路径上的点都染色成了c。

正当黄YY开心的完成了m次染色，准备在早上醒来之时向朋友们炫耀。但现实中的黄YY由于过于兴奋
滚到了床下，撞到了脑袋，在剧痛中醒来。由于脑部受到了严重创伤，黄YY对刚才梦境中发生的一切
发生了严重的信息丢失。

但英俊潇洒的黄YY当然不希望自己的窘态被朋友们发现。为了证明自己还是那个清明梦超能力者，他
希望告诉朋友们自己上色后每个节点的颜色。同时为了更进一步证明他还是个记忆大师，他希望干脆直
接说出每个点在倒数第k次染色时的颜色。

当然，现在的黄YY已经成了弱智了，作为黄YY最亲密的朋友，你快来帮帮黄YY吧！

Input

第一行三个整数n, m, k，代表树的点数，黄YY染色的次数，以及最后求颜色时，倒数的次数
（1 ≤ n, m, k ≤ 100000）。

接下来n − 1行，每行u, v代表u, v两点之间有一条边。这里保证1 ≤ u, v ≤ n，且无重边与自环，是一棵
标准的树。

接下来m行，每一行三个数字u, v, c代表黄YY在第这次用c颜色的画笔从u涂到了v。

Output

一行n个数字，输出每个点倒数第k次染色时的颜色。如果本身不足k次，输出0。

Example

standard input

3 3 2

1 2

2 3

1 2 1

2 3 2

1 3 3

standard output

1 2 2

Note

对于点1在第一次和第三次染色的时候分别被染色为1, 3，倒数第二次的颜色就是1。

对于点2在第一、二、三次染色的时候分别被染色为1, 2, 3，倒数第二次的颜色就是2。

对于点3在第二次和第三次染色的时候分别被染色为2, 3，倒数第二次的颜色就是2。

思路

首先每条路径从LCA处分开可以拆成两条链
假设链A->B执行了第i次染色操作，假设A是B的祖先，那么我们在B点加入一个”插入i”的事件，在A的父亲点加入一个”删除i”的事件
然后dfs整颗树求解，每个点维护一个线段树。处理一个点时先合并所有儿子的线段树，然后再处理这个点上的事件，得到线段树之后询问第K大值既可得到答案。
复杂度分析：
Node merge(Node a, Node* b) {
if (a == NULL) return b;
if (b == NULL) return a;
a->sum += b->sum;
a->child[0] = merge(a->child[0], b->child[0]);
a->child[1] = merge(a->child[1], b->child[1]);
return a;
}
考虑以上的线段树合并，每次合并会减少一个区间。而在事件点插入、删除的时候会产生至多log个区间，因此复杂度为O(NLogN)

Problem J. 最短路

给一个连通图，每次询问两点间最短路。每条边的长度都是1。

Input

第一行两个整数n和m，表示图的点数和边数（1 ≤ n ≤ 100000, 1 ≤ m ≤ n + 100）。

接下来m行每行两个整数a和b，表示一条边（1 ≤ a, b ≤ n）。保证没有自环和重边。保证图连通。

接下来一个整数q表示询问的个数（1 ≤ q ≤ 100000）。

接下来q行每行两个整数a和b表示询问a和b之间的最短路。

Output

每个询问输出一行表示答案

Example

input

4 5
1 2
2 3
1 4
4 3
2 4
4
1 4
1 2
2 4
1 3

output

1
1
1
2

思路

本题十分直接。我们不断地把度数为1的点删掉，把度数为2的点收缩，最后会得到一个图，和原图的点数与边数之差相同，且新图中每个点的度数都至少是3。这就是说我们会得到一个200个点300条边以内的图。新图可以用Floyd算法预处理所有点对之间最短路。询问时，将询问转化到新图上即可。转化时需要注意细节。

WANNAFLY_DAY2

Problem A. Tobaku Mokushiroku Kaiji

开司正在与另外一人玩石头剪刀布。双方各有一些代表石头、剪刀、布的卡牌，每局两人各出一张卡
牌，根据卡牌的内容决定这一局的胜负。胜负规则为：石头赢剪刀、剪刀赢布、布赢石头、相同为平
局。每张卡牌至多被使用一次。
已知双方的卡牌数量，问开司最多赢几局？

Input

一行六个数字a, b, c, d, e, f(0 ≤ a, b, c, d, e, f ≤ 50)，a, b, c分别表示开司的石头、剪刀、布的牌的数
量，d, e, f分别表示此时另一人的石头、剪刀、布的牌的数量。

Output

一个整数表示开司最多赢几局

Example

in

29 7 41 14 12 42

out

33

代码

1
2
3
4
5
6
7
8
9
#include<bits/stdc++.h>
using namespace std;
int main(){
	int a[6];
	for(int i = 0;i<6;i++)
		cin>>a[i];
	cout<<min(a[0],a[4])+min(a[1],a[5])+min(a[2],a[3])<<endl;
	return 0;
}

Problem E. Eustia of the Tarnished Wings

Novus Aither是一个潜藏着多个势力的城市。每个势力都有一个唯一的领导人，每个领导人有一个属性
值。如果两个势力的领导人的属性值分别为a, b，且|a − b| ≤ m，说明这两个领导人的思想有一定的相似
之处，这两个势力可以合并，新的领导人可以指定为原来的两个领导人中的任意一个。新产生的势力可
以依照相同的的规则，继续与其他势力合并。问在所有可能的合并情况中，最少会剩下几个势力。

Input

第一行两个空格隔开的整数n(1 ≤ n ≤ 106
), m(0 ≤ m109
)。n代表当前势力的个数。m的含义如题目描
述。
第二行n个空格隔开的整数di(0 ≤ di ≤ 109
)，代表第i个势力的领导人的属性值。

Output

输出一个数表示势力的最少数量。

Example
standard input
4 1
2 1 3 10

standard output

2

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn = 1e6+7;
ll a[maxn];
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	ll n,m;
	cin>>n>>m;
	for(int i = 0;i<n;i++){
		cin>>a[i];
	}
	sort(a,a+n);
	int cnt = 1;
	for(int i = 1;i<n;i++){
		if(a[i]-a[i-1]>m)
			cnt++;
	}
	cout<<cnt<<endl;
	return 0;
}

WANNAFLY_DAY3

Problem D. Shopping

你要买n件物品，其中有一些是凳子。
商场正在举行促销活动，如果购物车中有至少一个凳子，那么你可以半价购买这个购物车中最贵的一个
物品。
你有m辆购物车，请最小小化你的花费。

Input

第一行一个整数t表示数据组数(1 ≤ t ≤ 100)。

每组数据第一行两个整数n, m (1 ≤ n, m ≤ 1000)，接下来n行每行两个整数ai
, bi，分别表示第i件物品的
价格以及它是否是凳子(1 ≤ ai ≤ 105
, 0 ≤ bi ≤ 1)。

Output

每组数据输出一行一个实数表示最小花费，保留一位小数。

Example
stdin
2
5 1
1 0
2 1
3 1
4 0
5 0
5 10
1 0
2 1
3 1
4 0
5 0

stdout

12.5
10.5

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<bits/stdc++.h>
using namespace std;
int n,m;
const int maxn = 1007;
struct node{
	double cost;
	int flag;
}a[maxn];
int cmp(node a,node b){
	return a.cost>b.cost;
}
int main(){
	int t;
	cin >> t;
	while(t--){
		cin>>n>>m;
		int cnt = 0;
		double all = 0;
		for(int i = 0;i<n;i++){
			cin>>a[i].cost;
			cin>>a[i].flag;
			if(a[i].flag==1)
				cnt++;
			all+=a[i].cost;
		}
		if(cnt>m)
			cnt = m;
		sort(a,a+n,cmp);
		for(int i = 0;i<cnt;i++){
			all-=(a[i].cost/2.0);
		}
		printf("%.1lf\n",all);
	}
	return 0; 
}

WANNAFLY_DAY4

7 贵族用户

终于活成了自己讨厌的样子。
充钱能让你变得更强。

在暖婊这个游戏里面，如果你充了 x 元钱，那么你能获得 10x 个钻石。同时暖婊也有 m 档VIP，如果你往暖婊里面充了 ai 个钻石，那么你能成为第 i 档贵族用户。当你成为为第 i 档贵族用户。当你成为第 i 档贵族用户之后，那么你可以获得 pi% 的优惠。

你需要 k 件材料合成衣服，其中第 i 件材料原价为 di 个钻石，你一共需要 ci 件这种材料。
当你获得 p 的优惠时，这个材料的真实价格为 ⌈di(1 − p)⌉。
请问栗子米最少需要氪多少钱，这里我们规定只能氪整数的钱。

7.2 输入格式

第一行一个整数 T(T ≤ 1000)，表示数据组数。
每组数据第一行两个整数 m, k(1 ≤ m, k ≤ 15)。

接下来 m 行每行两个正整数 1 ≤ ai ≤ 105
, 1 ≤ pi ≤ 100，保证 ai < ai+1, pi ≤ pi+1。
接下来 k 行每行两个正整数 1 ≤ ci
, di ≤ 1000。

7.3 输出格式

对于每组数据，输出一个整数，表示至少要氪多少钱。

7.4 样例输入

1
1 1
100 100
100 100

7.5 样例输出

10

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include<bits/stdc++.h>
using namespace std;
int m,k;
struct node{
	int a;
	int p;
}vip[20];
struct cost{
	int cc;
	int dd;
}dim[20];
int main(){
	int t;
	cin>>t;
	while(t--){
		cin>>m>>k;
		for(int i = 0;i<m;i++){
			cin>>vip[i].a>>vip[i].p;
			if(vip[i].a%10)
				vip[i].a+=10-(vip[i].a%10);
		}
		int ans = 0;
		for(int i = 0;i<k;i++){
			cin>>dim[i].cc>>dim[i].dd;
			ans+=dim[i].cc*dim[i].dd;
		}
		if(ans%10)
			ans+=10-(ans%10);
		int minx = ans;
		for(int u = 0;u<m;u++){
			int ans2 = 0;
			for(int i = 0;i<k;i++){
				ans2 += dim[i].cc*(ceil((1-((double)vip[u].p/100.0))*dim[i].dd));
			}
			if(ans2%10){
				ans2+=10-(ans2%10);
			}
			if(ans2<=vip[u].a){
				ans2 = vip[u].a;
			}
			minx = min(minx,ans2);
		}
		cout<<minx/10<<endl;
	}
	return 0;
}

WANNAFLY_DAY6

F平衡二叉树

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 70;
ll n,d;
ll a,b;
ll c[maxn];
int main(){
	cin>>n>>d;
	a = 1;
	b = 0;
	memset(c,0,sizeof(c));
	for(int i = 0;i<n-1;i++)
		a*=2;
	a-=1;
	for(int i = 0;i<=d;i++){
		c[i] = 1;
	}
	c[d+1] = 2;
	for(int i = d+2;i<n-1-d;i++){
		c[i] = c[i-1]+c[i-d-1];
	}
	for(int i = 0;i<n-1-d;i++)
		b+=c[i];
	cout<<a-b<<endl;
	return 0;
}

H卡牌游戏

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include<bits/stdc++.h>
using namespace std;
int main(){
	int t;
	cin>>t;
	for(int u = 1;u<=t;u++){
		long double x,y;
		int z;
		cin>>x>>y;
		cin>>z;
		printf("Case #%d: ",u);
		long double ans = 0;
		for(int i = 0;i<z;i++){
			ans += x/y;
			x--;
			y--;
		}
		printf("%Lf\n",ans);
	}
	return 0;
}

WANNAFLY_DAY7

A.机器学习

https://qianyouyou-1258651414.cos.ap-chengdu.myqcloud.com/img/7WIGFX9JGWV%5DBD0A9XRS%5DG8.png

代码

1
2
3
4
5
6
7
8
#include<bits/stdc++.h>
using namespace std;
int main(){
	double n;
	cin>>n;
	printf("%.2lf\n",n);
	return 0;
}

D最小生成树

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 1e5+7;
ll a[maxn];
int main(){
	int n;
	cin>>n;
	ll minx = 0x3fffffff;
	ll sum = 0;
	for(int i = 0;i<n;i++){
		cin>>a[i];
		minx = min(minx,a[i]);
		sum+=a[i];
	}
	sum += minx*(n-1);
	sum-=minx;
	cout<<sum<<endl;;
	return 0;
}

G区间权值

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxx = 1e7+7;
const int maxn = 300007;
const int mod = 1e9+7;
ll a[maxn] = {0};
ll w[maxn] = {0};
ll dpa[maxn] = {0};
ll dpb[maxn] = {0};
ll dpl[maxn] = {0};
ll dpr[maxn] = {0};
int n;
void init(){
	for(int i = 1;i<=n;i++){
		int tmp = min(i,n-i+1);
		dpb[i] = tmp*dpa[n]%mod;
		dpb[i] -= dpl[tmp-1];
		dpb[i] -= dpr[n-tmp+2];
		dpb[i]%=mod;
		dpb[i] *= w[i];
		dpb[i]%=mod;
	}
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cin>>n;
	for(int i = 1;i<=n;i++){
		cin>>a[i];
		dpa[i] = a[i];
		dpa[i]+=dpa[i-1];
		dpa[i]%=mod;
		dpl[i] = dpl[i-1];
		dpl[i]+=dpa[i];
		dpl[i]%=mod;
	} 
	dpr[n+1] = 0;
	for(int i = n;i>=1;i--){
		dpr[i] = dpr[i+1];
		dpr[i]+=dpa[n]-dpa[i-1];
		dpr[i]%=mod;
	} 
	for(int i = 1;i<=n;i++){
		cin>>w[i];
	}
	ll ans = 0;
	init();
	for(int i = 1;i<=n;i++){
		ans+=dpb[i];
		ans%=mod;
	}
	cout<<ans<<endl;
	return 0;
}

I联通块计数

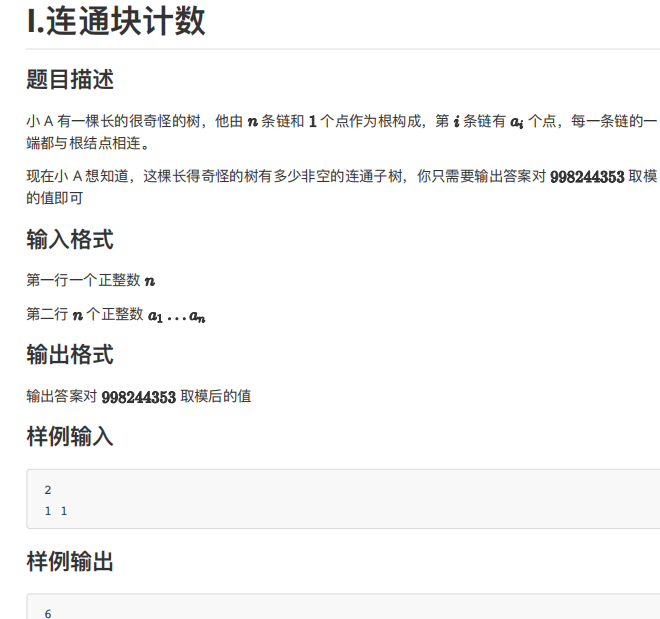
代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxx = 1e7+7;
const int maxn = 1e5+7;
const ll mod = 998244353;
int n;
ll a[maxn];
ll dp[maxn];
void init(){
	for(int i = 0;i<n;i++){
		dp[i] = a[i];
		dp[i]%=mod;
		if(i>0){
			dp[i]*=dp[i-1];
			dp[i]%=mod;
			dp[i]+=a[i];
			dp[i]%=mod;
			dp[i]+=dp[i-1];
			dp[i]%=mod;
		}
	}
}
int main(){
	cin>>n;
	ll ans = 1;
	for(int i = 0;i<n;i++){
		cin>>a[i];
		ans+=(a[i]*(a[i]+1)/2)%mod;
		ans%=mod;
		
	}
	init();
	if(n>0){
		ans+=dp[n-1];
		ans%=mod;
	}
	cout<<ans%mod<<endl;
	return 0;
}

J寻找复读机

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e3+7;
int n,m;
int vis[maxn];
int main(){
	cin>>n>>m;
	memset(vis,0,sizeof(vis));
	string str1, tmp;
	int d;
	while(m--){
		cin>>d;
		cin>>tmp;
		if(str1==tmp){
			if(vis[d]!=-1)
				vis[d]++;
		}
		else{
			vis[d]=-1;
		}
		str1 = tmp;
	}
	int flag = 0;
	for(int i = 1;i<=n;i++){
		if(vis[i]!=-1){
			if(flag==0){
				cout<<i;
				flag = 1;
			}
			else
				cout<<' '<<i;
		}
	}
	cout<<endl;
	return 0;
}
文章结束了，但我们的故事还在继续
坚持原创技术分享，您的支持将鼓励我继续创作！