定义
有一个有向图,每一个点都有一个权值(可以为正或负或0),选择一个权值和最大的子图,使得每个点的后继都在子图里面,这个子图就叫最大权闭合子图。
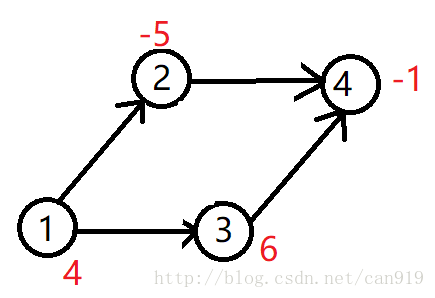
如下图:
能选的子图有Ø,{4},{3,4},{2,4},{1,2,3,4},它们的权值分别为0,-1,5,-6,4.
所以最大权闭合子图为{3,4},权值为5.
解法
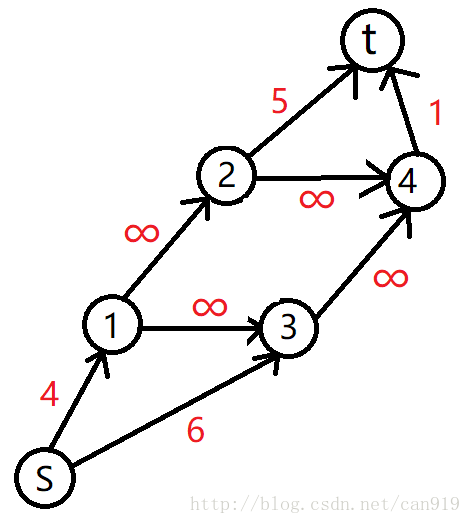
这个问题可以转化为最小割问题,用网络流解决。
从源点s向每个正权点连一条容量为权值的边,每个负权点向汇点t连一条容量为权值的绝对值的边,有向图原来的边容量全部为无限大。
求它的最小割,割掉后,与源点s连通的点构成最大权闭合子图,权值为(正权值之和-最小割)。
如何理解
割掉一条边的含义
由于原图的边都是无穷大,那么割边一定是与源点s或汇点t相连的。
割掉s与i的边,表示不选择i点作为子图的点;
割掉i与t的边,表示选择i点为子图的点。
如果s与i有边,表示i存在子图中;
如果i与t有边,表示i不存在于子图中。
合法性
只有s与t不连通时,才能得到闭合子图。
如果s与t连通,则存在点i,j,使得s到i有边,i到j连通,j到t有边,所以j一定是i的后继,但选择了i,没有选择j,不是闭合子图。
如果s与t不连通,选择了正权点i,一定选择了i后继中的所有负权点。设j是i的后继中的正权点,则割掉s到j的边是没有意义的,最小割不会割掉它,则j一点被选中,所以i的所有后继都被选中,符合闭合图的定义。
最优性
最小割=(不选的正权之和+要选的负权绝对值之和)
最大权闭合子图=(正权之和-不选的正权之和-要选的负权绝对值之和)=正权值和-最小割
因为正权值和,是定值,而最小割保证值最小,所以最大权闭合子图一定最优。
例题
POJ2987_Firing