[位运算]dfs+位运算解决N皇后问题

在N*N的方格棋盘放置了N个皇后，使得它们不相互攻击（即任意2个皇后不允许处在同一排，同一列，也不允许处在与棋盘边框成45角的斜线上。

你的任务是，对于给定的N，求出有多少种合法的放置方法。共有若干行，表示棋盘和皇后的数量；如果N=0，表示结束。

分析：

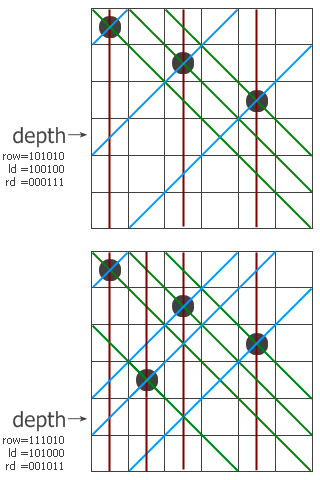
本篇文章重点介绍位运算解决N皇后的思想，并不是解决特定的问题。和普通算法一样，这是一个递归过程，程序一行一行地寻找可以放皇后的地方。过程带三个参数，row、ld和rd，分别表示在纵列和两个对角线方向的限制条件下这一行的哪些地方不能放。我们以6×6的棋盘为例，看看程序是怎么工作的。假设现在已经递归到第四层，前三层放的子已经标在左图上了。红色、蓝色和绿色的线分别表示三个方向上有冲突的位置，位于该行上的冲突位置就用row、ld和rd中的1来表示。把它们三个并起来，得到该行所有的禁位，取反后就得到所有可以放的位置。注意递归调用时三个参数的变化，每个参数都加上了一个禁位，但两个对角线方向的禁位对下一行的影响需要平移一位。最后，如果递归到某个时候发现row=111111了，说明六个皇后全放进去了，此时程序从第1行跳到第11行，找到的解的个数加一。

#include<stdio.h>  
#include<math.h>  
int N, Count, res;  
void dfs(int row, int ld, int rd) {  
    if (row == res) {  
        Count++;  
        return;  
    }  
    for (int j = 1; j <= res; j <<= 1)  
        if (row != (row | j) && ld != (ld | j) && rd != (rd | j))  
            dfs(row | j, (ld | j) << 1 & res, (rd | j) >> 1);  
}  
int main() {  
    while (~scanf("%d", &N), N) {  
        Count = 0;  
        res = pow(2, N) - 1;  
        dfs(0, 0, 0);  
        printf("%d\n", Count);  
    }  
    return 0;  
}