[图论]二分图匹配基本算法之KM算法解析

最佳匹配

如果一个二分图，X部和Y部的顶点数相等，若存在一个匹配包含X部与Y部的所有顶点，则称为完美匹配。

如果一个二分图，X部中的每一个顶点都与Y部中的一个顶点匹配，或者Y部中的每一个顶点也与X部中的一个顶点匹配，则该匹配为完备匹配。

带权二分图的权值最大的完备匹配称为最佳匹配。二分图的最佳匹配不一定是二分图的最大权匹配。 可以添加一些权值为0的边，使得最佳匹配和最大权匹配统一起来。 如图所示：

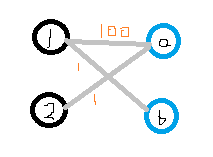
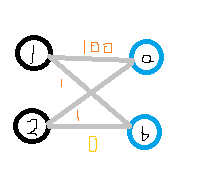
KM算法

求二分图的最佳匹配有一个非常优秀的算法,可以做到O(N^3),这就是KM算法。

1.首先选择顶点数较少的为X部，初始时对X部的每一个顶点设置顶标，顶标的值为该点关联的最大边的权值，Y部的顶点顶标为0。

2.对于X部中的每个顶点，在相等子图中利用匈牙利算法找一条增广路径，如果没有找到，则修改顶标，扩大相等子图，继续找增广路径。当每个点都找到增广路径时，此时意味着每个点都在匹配中，即找到了二分图的完备匹配。该完备匹配即为二分图的最佳匹配。

3.当X部的所有顶点都找到了增广路径后，则找到了完备匹配，此完备匹配即为最佳匹配。

相等子图

因为每个顶点有一个顶标，如果我们选择边权等于两端点的顶标之和的边，它们组成的图称为相等子图。

相等子图性质

1. 在任意时刻，相等子图上的最大权匹配一定小于等于相等子图的顶标和。
2. 在任意时刻，相等子图的顶标和即为所有顶点的顶标和。
3. 扩充相等子图后，相等子图的顶标和将会减小。
4. 当相等子图的最大匹配为原图的完备匹配时，匹配边的权值和等于所有顶点的顶标和，此匹配即为最佳匹配。

演示过程

1.如图所示，1与a匹配权值为3，与c为4。2与a权值为2，与b权值为1，与c权值为3。3与c权值为5。

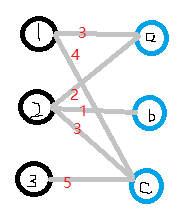
2.首先对每个顶点赋值，将左边的顶点赋值为最大权重，右边的顶点赋值为0。

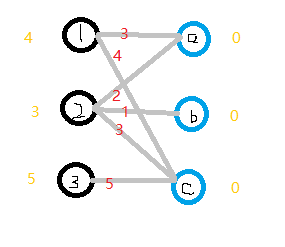
3.进行匹配，我们匹配的原则是：只与权重相同的边匹配，若是找不到边匹配，对此条路径的所有左边顶点-1，右边顶点+1，再进行匹配，若还是匹配不到，重复+1和-1操作。对1进行匹配，符合匹配条件的边只有1-c边。

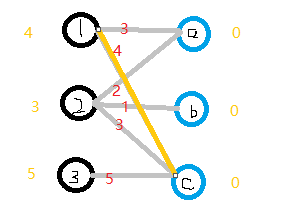
4.接着对2匹配，顶点2值为3，2-c边权重为3，但是，1已经匹配c了，发生了冲突，我们这时候第一时间应该想到的是，让2换个工作，但根据匹配原则，只有2-c边 3+0=0 满足要求，于是2不能换边了，那1能不能换边呢？对1来说，也是只有1-c边满足4+0=4的要求，于是1也不能换边，走投无路了，怎么办？

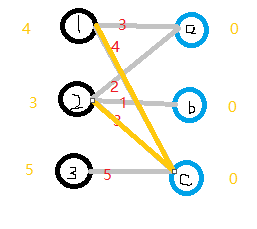
5.从常识的角度思考：其实我们寻找最优匹配的过程，也就是帮每个X顶点找到他们权值最高的Y顶点，但是，有些顶点会冲突，比如现在，1，2和c的权值都是最高，这时我们应该让1或者3换顶点，但是这时候换的话我们只能换到降低权值的Y顶点，也就是说，如果令R=左边顶点所有值相加，若发生了冲突，则最终权值一定小于R，但是，我们现在只要求最优匹配，所以，如果1换顶点降低的权值比较少的话，我们是能接受的（对2同样如此）。

在KM算法中如何体现呢？

现在参与到这个冲突的顶点是1,2和c，令所有左边顶点值-1，右边顶点值+1，即 1-1,2-1. c+1。

我们进行了上述操作后会发现，若是左边有n个顶点参与运算，则右边就有n-1个顶点参与运算，整体效率值下降了1*（n-（n-1））=1，而对于1来说，1-c本来为可匹配的边，现在仍为可匹配边（3+1=4），对于2来说，2-c本来为可匹配的边，现在仍为可匹配的边（2+1=4），我们通过上述操作，为1增加了一条可匹配的边1-a，为B增加了一条可匹配的边2-a。

现在我们再来匹配，对2来说，2-a边 2+0=2，满足条件，所以2换边，a现在为未匹配状态，2-a匹配！

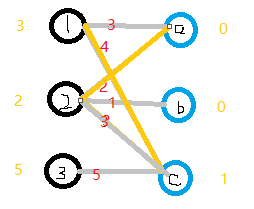
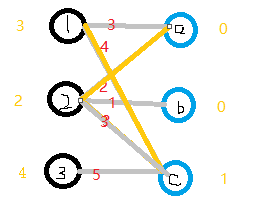
6.我们现在匹配最后一条边3，3-c 5+1！=5，3边无边能匹配，所以3-1。现在3-c边 4+1=5，可以匹配，但是c已匹配了，发生冲突，3此时不能换边，于是便去找1，对于1来说，1-a此时也为可匹配边，但是a已匹配，1又去找2。

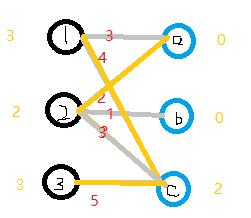
7.2现在无边可以匹配了，2+0！=1 ，现在的路径是3→c→1→a→2，所以1-1,2-1,3-1,a+1，c+1。如下图所示。

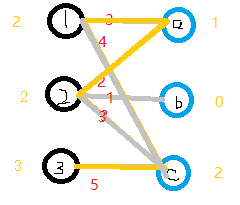
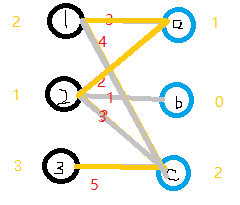
8.对于2来说，现在2-b 1+0=1 可匹配！使用匈牙利算法，对此条路径上的边取反。

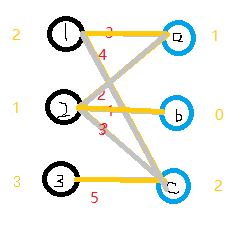
实现代码：

bool dfs(int s) //匈牙利算法找增广路径
{
    visx[s]=1;
    for(int i=1;i<=cnty;i++) 
        if(!visy[i]){
            int t=wx[s]+wy[i]-dis[s][i];
            if(t==0) {
                visy[i]=1;
                if(linky[i]==0||dfs(linky[i])){
                    linkx[s]=i,linky[i]=s;
                    return true;
                }
            }
            else if(t>0)  //找出边权与顶标和的最小的差值
            {
                if(t<minz)minz=t;
            }
        }
    return false;
}
void km()
{
    memset(linkx,0,sizeof linkx); //linkx[i]表示与X部中点i匹配的点
    memset(linky,0,sizeof linky);
    for(int i=1;i<=cntx;i++){
        while(1){
            minz=INF;
            memset(visx,0,sizeof visx);
            memset(visy,0,sizeof visy);
            if(dfs(i))break;
            for(int j=1;j<=cntx;j++)  //将交错树中X部的点的顶标减去minz
            if(visx[j])wx[j]-=minz;
            for(int j=1;j<=cnty;j++) //将交错树中Y部的点的顶标加上minz
            if(visy[j])wy[j]+=minz;
        }
    }
}