[数论]数论与与组合数学与线性代数中的常用算法总结

发表于 | 分类于 ， | 热度 ℃
字数统计: 3,159 | 阅读时长 ≈ 14

数论

欧几里得算法（gcd）

欧几里得算法又称辗转相除法，设两个数为a,b,则a,b最大公约数为gcd(a,b)=gcd(b,a%b)

证明

设a>=b, c = gcd( a, b), a = kc, b = jc,则k,j互素（否则c不为a，b最大公约数），则设 r = a % b,则a = mb + r,则r = a - mb = kc - mjc = ( k - mj ) c，因为k,j互素，则k-mj与j互素，gcd(a,b) = gcd(b,a%b)

应用

如果判断两个数是否互素(最大公约数为1)，这时辗转相除法就方便得多。因为每一步都是取模，保证了数据减小的速度特别快。能够在很短时间内找到最大公约数。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//递归版
int gcd(int a, int b) {
	return b ? a : gcd(b, a%b);
}
//非递归版
int gcd(int a, int b) {
	if (!a)
		return b;
	while (b) {
		int temp = b;
		b = a%b;
		a = temp;
	}
	return a;
}

扩展欧几里得算法（exgcd）

若a , b 不全为 0，则存在整数 x,y 使得 gcd(a,b)=xa+yb
对于辗转相除法的最后一项,此时 b=0,则 gcd(a,b)=1a+0b,因为 gcd(a,b)=gcd(b,a%b)则有 xa+yb=x1b+y1(a%b) 。将等式右边变形，bx1+(a%b)y1=bx1+(a-(a/b)b)y1=ay1+b(x1-(a/b)y1)
则，x=y1,y=x1-(a/b)*y1 则可由后向前迭代得到 x,y

应用

对于扩展欧几里德定理的题，一般都需要进行一定的推导之后得到一个形式为xa+yb=c 的方程，然后根据 c 确定解是否存在，如果 c 可以被 gcd(a,b)整除，那么方程有解，否则方程无解。而且所得的解释不唯一的，对于一组解 x0,y0 则其所有解可以表示为x=x0+b/gcd(a,b)t,y-y0-a/gcd(a,b)t,t=0,+1,+2……一般会要求找出 x 或者 y 的最小正整数解，这个时候需要做一些调整。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int exgcd(int a, int b, int &x, int &y)
{
	if (b == 0)
	{
		x = 1;
		y = 0;
		return a;
	}
	int d = exgcd(b, a%b, x, y);
	int t = x;
	x = y;
	y = t - a / b*y;
	return d;
}

筛法求素数

筛素数的基本方法是用来筛选出一定范围内的素数

原理

利用素数只有1和本身两个约数，且约数一定不大于自身。首先筛掉1.剩下的数选择最小的数为素数，然后筛掉它范围内所有的倍数，以此类推，直到筛为空时结束。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
bool isprime[N];//N 表示范围
int prime[N], cnt;
void f()
{
	int i, j;
	cnt = 0;
	memset(isprime, true, sizeof(isprime));
	isprime[1] = false;
	for (i = 2; i <= N; i++)
	{
		if (isprime[i])
		{
			prime[cnt++] = i;//记录素数
			for (j = i*i; j <= N; j += i)//因为小于 i 的所有的倍数都被筛过，所以直接从 i*i 开始，从这里也可以看出，筛素数时到 N^0.5就可以了
				isprime[j] = false;
		}
	}
}

快速幂

快速幂的目的就是做到快速求幂，假设我们要求a^b,按照朴素算法就是把a连乘b次，这样一来时间复杂度是O(n)级别，快速幂能做到O(logn)。

原理

　　假设我们要求a^b，那么其实b是可以拆成二进制的，该二进制数第i位的权为2^(i-1)，例如当b==11时，a11=a(2^0+2^1+2^3)。11的二进制是1011，11 = 2³×1 + 2²×0 + 2¹×1 + 2º×1，因此，我们将a¹¹转化为算 a2^0a2^1a2^3，也就是a1 a2 a8，原来算11次，现在算三次，但是这三项貌似不好求的样子….不急，下面会有详细解释。由于是二进制，很自然地想到用位运算这个强大的工具：&和>>。&运算通常用于二进制取位操作，例如一个数 & 1 的结果就是取二进制的最末位。还可以判断奇偶x&1==0为偶，x&1==1为奇。>>运算比较单纯,二进制去掉最后一位，不多说了，先放代码再解释。

1
2
3
4
5
6
7
8
9
10
int poww(int a, int b) {
    int ans = 1, base = a;
    while (b != 0) {
        if (b & 1 != 0)
            ans *= base;
        base *= base;
        b >>= 1;
    }
    return ans;
}

以b==11为例，b=>1011,二进制从右向左算，但乘出来的顺序是 a^(2^0)a^(2^1)a^(2^3)，是从左向右的。我们不断的让base*=base目的即是累乘，以便随时对ans做出贡献。

　　其中要理解base =base这一步：因为 base base==base2，下一步再乘，就是base2 base2==base4，然后同理 base4 base4=base8，由此可以做到base–>base2–>base4–>base8–>base16–>base32…….指数正是 2^i ，再看上面的例子，a¹¹= a1a2a8，这三项就可以完美解决了

矩阵快速幂

矩阵乘法

简单的说矩阵就是二维数组，数存在里面，矩阵乘法的规则:A*B=C

img

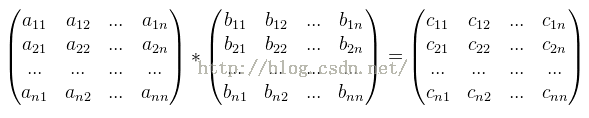
其中c[i][j]为A的第i行与B的第j列对应乘积的和，即: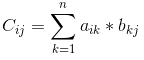img

1
2
3
4
5
6
7
8
9
10
const int N=100;  
int c[N][N];  
void multi(int a[][N],int b[][N],int n)//n是矩阵大小，n<N  
{  
    memset(c,0,sizeof c);  
    for(int i=1;i<=n;i++)  
        for(int j=1;j<=n;j++)  
        for(int k=1;k<=n;k++)  
        c[i][j]+=a[i][k]*b[k][j];  
}

方法很简单，把快速幂算法中的乘法改成矩阵的乘法就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
const int N=10;  
int tmp[N][N];  
void multi(int a[][N],int b[][N],int n)  
{  
    memset(tmp,0,sizeof tmp);  
    for(int i=0;i<n;i++)  
        for(int j=0;j<n;j++)  
        for(int k=0;k<n;k++)  
        tmp[i][j]+=a[i][k]*b[k][j];  
    for(int i=0;i<n;i++)  
        for(int j=0;j<n;j++)  
        a[i][j]=tmp[i][j];  
}  
int res[N][N];  
void Pow(int a[][N],int n)  
{  
    memset(res,0,sizeof res);//n是幂，N是矩阵大小  
    for(int i=0;i<N;i++) res[i][i]=1;  
    while(n)  
    {  
        if(n&1)  
            multi(res,a,N);//res=res*a;复制直接在multi里面实现了；  
        multi(a,a,N);//a=a*a  
        n>>=1;  
    }  
}

下面放一个求斐波那契数列的矩阵快速幂模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
const int mod = 10000;
const int maxn = 35;
int N;
struct Matrix {
    int mat[maxn][maxn];
    int x, y;
    Matrix() {
        memset(mat, 0, sizeof(mat));
        for (int i = 1; i <= maxn - 5; i++) mat[i][i] = 1;
    }
};
inline void mat_mul(Matrix a, Matrix b, Matrix &c) {
    memset(c.mat, 0, sizeof(c.mat));
    c.x = a.x; c.y = b.y;
    for (int i = 1; i <= c.x; i++) {
        for (int j = 1; j <= c.y; j++) {
            for (int k = 1; k <= a.y; k++) {
                c.mat[i][j] += (a.mat[i][k] * b.mat[k][j]) % mod;
                c.mat[i][j] %= mod;
            }
        }
    }
    return ;
}
inline void mat_pow(Matrix &a, int z) {
    Matrix ans, base = a;
    ans.x = a.x; ans.y = a.y;
    while (z) {
        if (z & 1 == 1) mat_mul(ans, base, ans);
        mat_mul(base, base, base);
        z >>= 1;
    }
    a = ans;
}
int main() {
    while (cin >> N) {
        switch (N) {
            case -1: return 0;
            case 0: cout << "0" << endl; continue;
            case 1: cout << "1" << endl; continue;
            case 2: cout << "1" << endl; continue;
        }
        Matrix A, B;
        A.x = 2; A.y = 2;
        A.mat[1][1] = 1; A.mat[1][2] = 1;
        A.mat[2][1] = 1; A.mat[2][2] = 0;
        B.x = 2; B.y = 1;
        B.mat[1][1] = 1; B.mat[2][1] = 1;
        mat_pow(A, N - 1);
        mat_mul(A, B, B);
        cout << B.mat[1][1] << endl;
    }
    return 0;
}

欧拉函数

φ(x)=x(1-1/p1)(1-1/p2)(1-1/p3)(1-1/p4)…..(1-1/pn),其中 p1, p2……pn 为 x 的所有质因数。

设 p 是素数 a 是一个正整数 φ(p^a)=p^a-p^a-1; m 与 n 互素 φ(mn)=φ(m)φ(n); φ(n)=n sum(1-1/pi)/pi 是与 n 的质因子n 为奇数时 φ(2n)=φ(n)。

模运算

基本的模运算

(a + b)mod n=((a mod n) + (b mod n))mod n;

(a - b)mod n=((a mod n) - (b mod n))mod n;

(a b)mod n=((a mod n) (b mod n))mod n;

数论4大定理

威尔逊定理

若p为质数，则p可整除(p-1)!+1。

欧拉定理

若n,a为正整数，且n,a互素，即gcd(a,n) = 1，则a^φ(n) ≡ 1 (mod n)

证明

设x（1），x（2），…，x(φ(n))是一个以n为模的简系，则ax（1），ax（2），…，ax（φ(n) ）也是一个以n为模的简系（因为（a，n）=1）。

于是有ax（1）ax（2）…ax（φ(n) ）≡x（1）x（2）…x(φ(n))（mod n），

所以a^φ(n) ≡ 1 (mod n)。

费马小定理

假如p是质数，若p不能整除a，则 a^(p-1) ≡1（mod p），若p能整除a，则a^(p-1) ≡0（mod p）。

若p是质数，且a,p互质，那么 a的(p-1)次方除以p的余数恒等于1。

证明

因为p是质数，且（a，p)=1，所以φ(p)=p-1。由欧拉定理可得a^(p-1) ≡1（mod p）。证毕。对于该式又有a^p ≡a（mod p），所以，费马小定理的另一种表述为：假如p是质数，且(a,p)=1，那么a^p ≡a（mod p）。

孙子定理（中国剩余定理）

高斯消元

高斯消元法，是线性代数中的一个算法，可用来为线性方程组求解，求出矩阵的秩，以及求出可逆方阵的逆矩阵。当用于一个矩阵时，高斯消元法会产生出一个“行梯阵式”。利用矩阵化成的行阶梯型可以方便的得出未知数的解。

要用高斯消元，一般也会需要一定的推理，得出线性方程组，再利用高斯消元求解。

组合数学

排列组合

加法原理

加法原理：做一件事，完成它可以有 n 类办法，第一类办法的方法属于集合 A1，第二类办法的方法属于集合 A2，……，第 n 类办法的方法属于集合 An，那么完成这件事的方法属于集合 A1UA2U…UAn。

分类的要求 ：每一类中的每一种方法都可以独立地完成此任务；两类不同办法中的具体方法，互不相同（即分类不重）；完成此任务的任何一种方法，都属于某一类（即分类不漏）

乘法原理

乘法原理：做一件事，完成它需要分成 n 个步骤，做第一步有 m1 种不同的方法，做第二步有 m2 种不同的方法，……，做第 n 步有 mn 种不同的方法，那么完成这件事共有N=m1×m2×m3×…×mn 种不同的方法。

合理分步的要求,任何一步的一种方法都不能完成此任务，必须且只须连续完成这 n 步才能完成此任务；各步计数相互独立；只要有一步中所采取的方法不同，则对应的完成此事的方法也不同。

公式

排列的定义及其计算公式：从 n 个不同元素中，任取 m(m≤n,m 与 n 均为自然数,下同）个元素按照一定的顺序排成一列，叫做从 n 个不同元素中取出 m 个元素的一个排列；从 n 个不同元素中取出 m(m≤n）个元素的所有排列的个数，叫做从 n 个不同元素中取出m 个元素的排列数，用符号 A(n,m）表示。A(n,m)=n(n-1)(n-2)……(n-m+1)= n!/(n-m)! 此外规定 0!=1

组合的定义及其计算公式：从 n 个不同元素中，任取 m(m≤n）个元素并成一组，叫做从 n 个不同元素中取出 m 个元素的一个组合；从 n 个不同元素中取出 m(m≤n）个元素的所有组合的个数，叫做从 n 个不同元素中取出 m 个元素的组合数。用符号 C(n,m) 表示。C(n,m)==A(n,m)/m！；C(n,m)=C(n,n-m）。（n>=m)

其他排列与组合公式 从 n 个元素中取出 m 个元素的循环排列数=A(n,m)/m=n!/m(n-m)!. n 个元素被分成 k 类，每类的个数分别是 n1,n2,…nk 这 n 个元素的全排列数为 n!/(n1！×n2！×…×nk!). k 类元素，每类的个数无限，从中取出 m 个元素的组合数为 C(m+k-1,m）。

容斥原理

设 A1,A2 为有限集合，其元素个数分别为|A1|，|A2|,则| A1∪A2|=| A1+A2|-| A1∩A2|
这个定理，常称作包含排斥原理，也就是容斥原理。

对于需要用到容斥原理的题型，一般都比较容易看出来用的方法，而且一般采用深搜的方法进行运算

文章结束了，但我们的故事还在继续
坚持原创技术分享，您的支持将鼓励我继续创作！