[计算几何]二维计算几何基础

发表于 | 分类于 ， | 热度 ℃
字数统计: 4,211 | 阅读时长 ≈ 19

三寸青笺，写不尽对你的思念。——随笔

用解析几何借助计算机处理几何问题存在着两大缺陷：

1）方程解的情况复杂，例如Ax+By+C=0；

2）存在着浮点误差积累。

计算几何采用了介于代数与几何之间的方式解决几何问题。它利用几何特性辅助简单的代数运算解决几何问题，既能精确求解，有提高了算法效率，并且不失几何的优美特性。

向量

向量

向量：既有大小又有方向的量。

向量的比较

在平面坐标系下，某点的坐标用（x，y）表示，向量和点一样，也可以用x,y表示。

1
2
3
4
5
struct Point{	//点
    double x,y;
    Point(double x=0,double y=0):x(x),y(y) {}	//构造函数方便代码编写
};
typedef Point Vector;	//向量。从程序实现上，Vector只是Point的别名

向量的加减乘除

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//向量+向量=向量，点+向量=点
Vector operator + (Vector A, Vector B) {
	return Vector(A.x + B.x, A.y + B.y);
}
//点-点=向量
Vector operator - (Point A, Point B) {
	return Vector(A.x - B.x, A.y - B.y);
}
//向量*数=向量
Vector operator * (Vector A, double p) {
	return Vector(A.x * p, A.y * p);
}
//向量/数=向量
Vector operator / (Vector A, double p) {
	return Vector(A.x / p, A.y / p);
}

向量的比较

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
bool operator < (const Point& a, const Point& b) {
	return a.x < b.x || (a.x == b.x&&a.y < b.y);
}
//减下误差的必要比较
const double eps=1e-8;
int dcmp(double x)
{
    if(fabs(x)<eps) return 0;
    if(x>0) return 1;
    return -1;
}
bool operator ==(const point& a,const point& b)
{
    return dcmp(a.x-b.x)==0&&dcmp(a.y-b.y)==0;
}

注意上面的“相等”函数用到“三态函数”dcmp,减少了精度问题。另外，向量有一个所谓的“极角”，即从x轴正半轴旋转到该向量方向所需要的角度。C标注库里的atan2函数就是用来求极角的。如向量（x,y）的极角就是atan2（y，x）（单位：弧度）

向量內积（点积）

点积，向量α和β的点积等于二者长度的乘积再乘上它们夹角的余弦。当夹角大于90°时点积为负。两向量的点积为一个标量 α·β，它的大小为α·β=|α||β|cosθ，其中θ是<α,β>

余弦为偶函数，因此点积满足交换率。如果两向量垂直，点积为0。

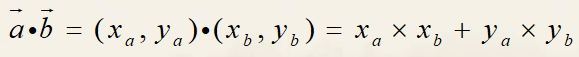
几何意义

α在β的投影α’与β的长度乘积

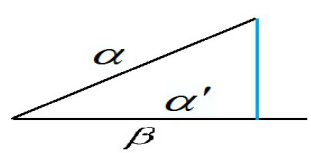
由定义易知当两向量夹角为锐角时点积值为正，夹角钝角为负，垂直为0

1
2
3
4
5
6
7
8
9
double dot(Vector A,Vector B){    //向量点积
    return A.x*B.x+A.y*B.y;
}
double Length(Vector A){    //向量A长度
    return sqrt(dot(A,A));
}
double angle(Vector A,Vector B){    //向量A和B夹角
    return acos(dot(A,B)/Length(A)/Length(B));
}

向量外积（叉积）

简单地说，两个向量u和w得叉积等于u和w组成的三角形的有向面积的两倍。

叉积的二维意义—-有向面积：外积大小为由u，w这两个向量围成的平行四边形有向面积。

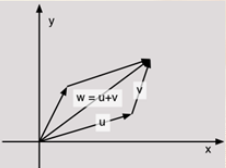
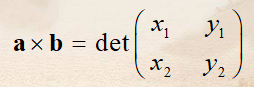
两向量的叉积为一个矢量 a×b，设向量 P(x1,y1),Q(x2,y2)，向量 a 和向量 b 的叉积还是一个向量，长度为|PQ|=x1y2-x2y1;即为向量 P,Q 围成的四边形的面积。它的方向与向量PQ 垂直，并且使(P,Q,P×Q)成右手系。

几何意义

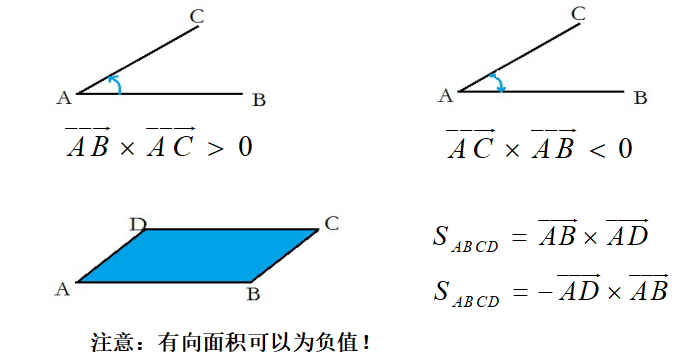
不难发现，叉积不满足交换率，cross（u，w）=-corss（w，u）。

1
2
3
4
5
6
7
8
double cross(Vector A,Vector B)  //叉积
{
    return A.x*B.y-A.y*B.x;
}
double area(point A,point B,point C)	//已知三个点 p0,p1,p2 的叉积函数
{
    return cross(B-A,C-A);
}

叉积的一个重要性质，判断两向量互相之间的顺逆时针关系。
若 P×Q>0，则P在Q 的顺时针方向；
若 P×Q<0，则P在Q 的逆时针方向；
若 P×Q=0，则P和Q 共线，但可能同向也可能反向；

利用这一性质，可以将一个多边形的顶点按照顺时针或者逆时针方向排序，这就是极角排序。利用 sort 或者 qsort 函数，自己定义 cmp 函数即可。

1
2
3
4
5
6
7
8
9
10
//逆时针极角排序比较函数(double) 
bool cmp(const point &a, const point &b) { 
double x = atan2(a.y, a.x), y = atan2(b.y, b.x); 
return x < y; 
} 
//象限极角排序比较函数(int)，不失精度 
int cross(point p1,point p2,point p0){ 
return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y); 
} 
sort(p+1,p+n,cmp);

两向量的位置关系

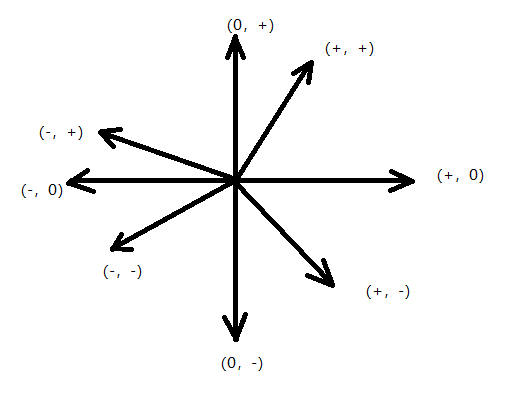
把叉积和点积组合在一起，很容易判断两向量的位置关系。如图所示，括号第一个数是点积的符号，第二个是叉积的符号。第一个向量u总是向右，另一个向量w的各种情况都包含在了图中。比如当w的中点在下图左上方的第二象限时点积为负担叉积均为正，用（-，+）表示。

点和直线

点到直线的距离

点到直线的距离是一个常用函数，可以用叉积求出，即用平行四边形的面积除以底。代码如下：

1
2
3
4
5
double DistoLine(point P,point A,point B) //点p到直线AB距离
{
    Vector v1=B-A,v2=P-A;
    return fabs(cross(v1,v2))/Length(v1);	//如果不取绝对值，得到的是有向距离
}

点到线段的距离

点到线段有两种可能：

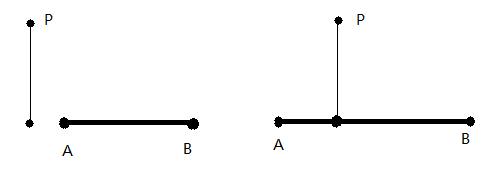
简单地说，设投影点为Q，如果Q在线段AB上，则所求距离就是P点直线AB的距离（右）。如果Q在射线BA上，则所求为PA距离；否则为PB距离。判断Q的位置可以用点积进行。

1
2
3
4
5
6
7
double DistoSegment(point P,point A,point B){
    if(A==B) return Length(P-A);
    Vector v1=B-A,v2=P-A,v3=P-B;
    if(dcmp(dot(v1,v2))<0) return Length(v2);
    if(dcmp(dot(v1,v3))>0) return Length(v3);
    return fabs(cross(v1,v2))/Length(v1);
}

判断点是否在线段上

判断点 Q 在线段 P1P2 上的两条依据：
①(Q-P1)*(P2-P1)=0;
②Q 在以 P1,P2 为对角顶点的矩形内。 

1
2
3
4
5
bool onSegment(point p1,point p2,point Q){
if( (Q.x-p1.x)*(p2.y-p1.y)==(p2.x-p1.x)*(Q.y-p1.y)&&min(p1.x,p2.x)<=Q.x&&Q.x<=max(p1.x,p2.x)&&min(p1.y,p2.y)<=Q.y&&Q.y<= max(p1.y,p2.y) )
return 1;
else return 0;
}

线段相交

最为直观的想法：解析几何法

弊端：运算误差大，运算次数多

误差来源：浮点运算

另外，编程难度事实上也很大（区域判断）

计算几何做法：运用叉积点积和位置关系

线段规范相交

定义线段规范相交为两线段相交恰好有一个公共点且不是任一线段的端点

充要条件：每条线段的两个端点都在另一条线段的两侧

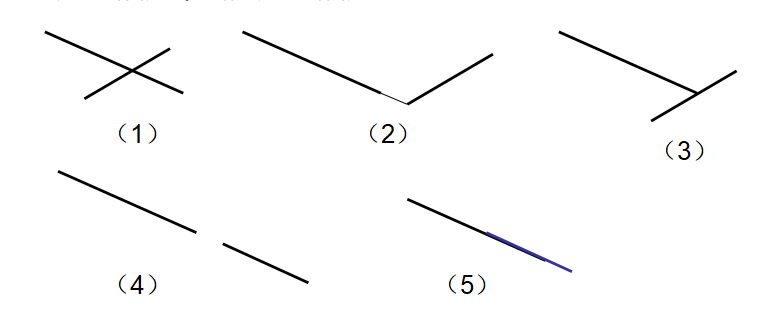
只有（1）是规范相交，其它是非规范相交。非规范相交的情况还有很多。

跨立实验

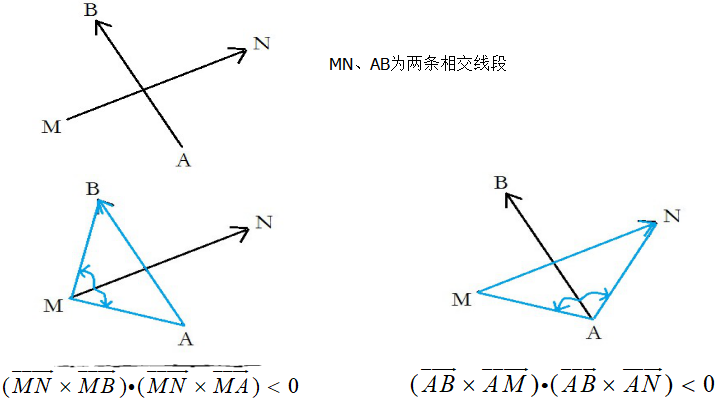
规范相交
1
2
3
4
5
6
bool SegmentItersection(point a1, point a2, point b1, point b2)
{
    double c1 = cross(a2-a1, b1-a1), c2 = cross(a2-a1, b2-a1),
    c3 = cross(b2-b1, a1-b1), c4 = cross(b2-b1, a2-b1);
    return dcmp(c1)*dcmp(c2) < 0 && dcmp(c3)*dcmp(c4) < 0;
}
线段相交

如果允许在端点处相交怎么办？

首先可能共线重叠

其次就是交点是端点

如果交点是端点

就判断几次点是否在线段上

1
2
3
4
5
//判断点p是否在线段a1 a2上
bool OnSegment(point p,point a1,point a2)
{
  return dcmp(cross(a1-p,a2-p))==0&&dcmp(dot(a1-p,a2-p))<0; //线段包含端点时改成<=
}

多边形问题

多边形面积

两向量的叉积的几何意义是以这两个向量为邻边的平行四边形的有向面积，我们可以利用这一点来求简单多边形的面积。所谓简单多边形就是任何不相邻的两条边都没有交点，包括凸多边形和凹多边形。

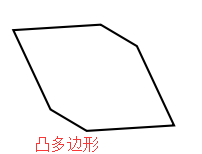
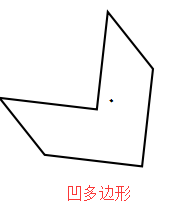
求下面多边形的面积，已知个顶点的坐标。

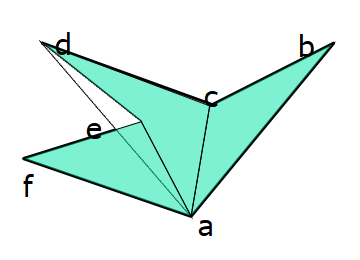
注意：在引入叉积后，面积就可以为负值，就有了“负面积”的概念。“负面积”方便了我们的运算。

可以取p[0]点为划分顶点，一方面可以少算两个叉积（0和任何向量的叉积都等于0），另一方面也减少乘法溢出的可能性，还不用特殊处理（i=n-1时，下一个顶点p[0]而不是p[n]，因为p[n]不存在）

1
2
3
4
5
6
7
8
//取p[0]为划分顶点
double PolygonArea(vector<Point> p) {
  int n = p.size();
  double area = 0;
  for(int i = 1; i < n-1; i++)
    area += Cross(p[i]-p[0], p[i+1]-p[0]);
  return area/2;
}

也可以取坐标原点为划分点，乘法次数减少。

点在多边形内外判断

判断点是否在三角形内

点 P 在三角形 ABC 内部常用的又两种方法，面积法和叉积法，面积法即为

S△PAB+S△PAC+S△PBC=S△ABC

其中三角形面积计算公式为 S=1/2×|cross(a,b)|

叉积法

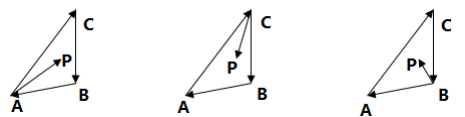
利用叉积的正负号判断，如图所示，AP 在向量 AC 的顺时针方向，CP 在向量 BC 的顺时针方向，BP 在向量 BC 的顺时针方向，利用这一性质推广，那么可以利用叉积的正负号来判断一个点是否在一个凸多边形内部。

判断点是否在多边形内

一般而言，该问题有射线法和转角法两种处理手段

射线法：从这个点出发引向无穷远点一条直线，根据交点情况确定点的位置

转角法：计算多边形每条边的转角，若最后相消为0则在外部，否则在内部

射线法：特殊情况不易处理

转角法：三角运算时间开销大

射线法

以要判断的点为起点任作一射线，计算该射线与多边形的交点数目。

若有偶数个交点则在形外，否则在形内。

若与线段在端点处相交或重合，则要进行复杂的判断。此时可另取一射线。

转角法

把多边形每条边的转角加起来，如果是360度，就在多边形内，如果是0度就在外面，180度则是在边界上

直接最要求角度用到反三角函数精度差且费时

改进

假设有一条向右的射线，统计多边形穿过这条射线正反多少次，把这个数记为绕数wn，逆时针穿过时，wn加1，顺时针穿过时，wn减1。

注意在程序实现时，判断是否穿过，以及穿过方向时，需要用叉积判断输入点在左边还是右边。

实现代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int isPointinPolygon(point p,vector<point>poly)
{
    int wn=0;
    int n=poly.size();
    for (int i=0;i<n;i++)
    {
        if (OnSegment(p,poly[i],poly[(i+1)%n])) return -1;    //边界
        int k=dcmp(Cross(poly[(i+1)%n]-poly[i],p-poly[i]));
        int d1=dcmp(poly[i].y-p.y);
        int d2=dcmp(poly[(i+1)%n].y - p.y);
        if (k>0&&d1<=0&&d2>0) wn++;
        if (k<0&&d2<=0&&d1>0) wn--;
    }
    if (wn!=0) return 1;  //内部
    return 0;   //外部
}

点在凸多边形内的判定更简单，只需判断是否在所有边的左边（假设各个顶点按照逆时针顺序排列）

多边形重心

三角形重心

多边形重心

将多边形拆分为N个三角形，分别求其重心和面积，可以想象，原来的质量均匀分布在内部的区域上，而现在质量仅分布在这N个重心点上（等价变换），这时就可以利用刚才猜想的公式了。

1
2
3
4
5
6
7
8
9
10
11
12
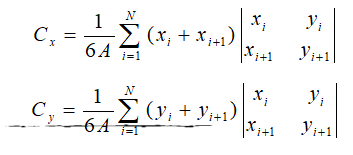
13
point PolyGravity(point *p,int n)
{
    point ans=point(0,0);
    double sumArea=0,area;
    for(int i=2;i<n;i++)
    {
        area=cross(p[i-1]-p[0],p[i]-p[0]);
        sumArea+=area;
        ans.x+=(p[0].x+p[i-1].x+p[i].x)*area;
        ans.y+=(p[0].y+p[i-1].y+p[i].y)*area;
    }
    return ans/(sumArea*3);
}

解析几何

交点的计算：求两线段，两直线，线段和直线的交点
①判断两线段是否相交：
我们分两步确定两条线段是否相交：
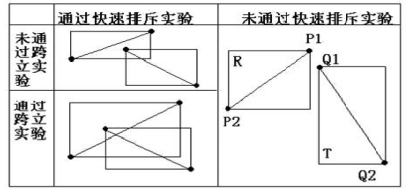
(1)快速排斥试验
设以线段 P1P2 为对角线的矩形为 R， 设以线段 Q1Q2 为对角线的矩形为 T，如果R和T不相交，显然两线段不会相交。
(2)跨立试验
如果两线段相交，则两线段必然相互跨立对方。若 P1P2 跨立 Q1Q2 ，则矢量 ( P1 - Q1 ) 和( P2 - Q1 )位于矢量( Q2 - Q1 ) 的两侧，即 ( P1 - Q1 ) × ( Q2 - Q1 ) ( P2 - Q1 ) × ( Q2 - Q1 ) < 0。
上式可改写成 ( P1 - Q1 ) × ( Q2 - Q1 ) ( Q2 - Q1 ) × ( P2 - Q1 ) > 0。
当 ( P1 - Q1 ) × ( Q2 - Q1 ) = 0 时，说明 ( P1 - Q1 ) 和 ( Q2 - Q1 )共线，但是因为已经通过快速排斥试验，所以 P1 一定在线段 Q1Q2 上；同理，( Q2 - Q1 ) ×(P2 - Q1 ) = 0 说明 P2 一定在线段 Q1Q2 上。所以判断 P1P2 跨立 Q1Q2 的依据是：

( P1 - Q1 ) × ( Q2 - Q1 ) ( Q2 - Q1 ) × ( P2 - Q1 ) >= 0。
同理判断 Q1Q2 跨立 P1P2 的依据是：
( Q1 - P1 ) × ( P2 - P1 ) ( P2 - P1 ) × ( Q2 - P1 ) >= 0。

另外，“规范相交”指的是两条线段恰有唯一一个不是端点的公共点；而如果一条线段的一个端点在另一条线段上，或者两条线段部分重合，则视为“非规范相交”，以下代码是“非规范相交”。

结合 poj2653 练习，代码可参考：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
const double eps = 1e-10;
struct point { double x, y; };
struct Line { point begin, end; }line[100001];
double min(double a, double b) { return a<b ? a : b; }
double max(double a, double b) { return a>b ? a : b; }
bool inter(const Line & M, const Line & N) {
	point a = M.begin; point b = M.end;
	point c = N.begin; point d = N.end;
	if (min(a.x, b.x) > max(c.x, d.x) || min(a.y, b.y)>max(c.y, d.y) || min(c.x, d.x)>max(a.x, b.x) || min(c.y, d.y) > max(a.y, b.y)) return 0;
	double h, i, j, k;
	h = (b.x - a.x)*(c.y - a.y) - (b.y - a.y)*(c.x - a.x);
	i = (b.x - a.x)*(d.y - a.y) - (b.y - a.y)*(d.x - a.x);
	j = (d.x - c.x)*(a.y - c.y) - (d.y - c.y)*(a.x - c.x);
	k = (d.x - c.x)*(b.y - c.y) - (d.y - c.y)*(b.x - c.x);
	return h*i <= eps&&j*k <= eps;
}

②判断两直线是否相交：
首先判断两条直线是否在一条直线上，或者两条直线平行，否则一定相交，不平行且不在一条直线上则相交并且求出交点。
可结合 hrbustoj1104 练习，代码可参考： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include<stdio.h> 
int main() {
	int t;
	double x1, x2, x3, x4, y1, y2, y3, y4, x, y;
	scanf("%d", &t);
	while (t--) {
		scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
		scanf("%lf%lf%lf%lf", &x3, &y3, &x4, &y4);
		if ((x2 - x1)*(y4 - y3) == (x4 - x3)*(y2 - y1)) {
			if ((x3 - x1)*(y4 - y2) == (x4 - x2)*(y3 - y1) && (y4 - y3) != 0)
				puts("LINE");//在一条直线的情况 
			else
				puts("NONE");//平行的情况 
		}
		else {
			x = ((y1*(x2 - x1) - x1*(y2 - y1))*(x4 - x3) - (y3*(x4 - x3) - x3*(y4 -
				y3))*(x2 - x1)) / ((y4 - y3)*(x2 - x1) - (y2 - y1)*(x4 - x3));
			y = ((y1*(x2 - x1) - x1*(y2 - y1))*(y4 - y3) - (y3*(x4 - x3) - x3*(y4 -
				y3))*(y2 - y1)) / ((y4 - y3)*(x2 - x1) - (y2 - y1)*(x4 - x3));
			printf("POINT %.2f %.2f\n", x, y);
		}
	}
	return 0;
}

③判断线段和直线的交点：
poj1039 判断直线和线段是否相交并求出交点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#define eps 1.0e-8 
struct Point {
	double x, y;
} point[25];
int n;
double ans;
bool ok;
double intersect(Point a1, Point b1, Point a2, Point b2) {
	double x1 = a1.x, x2 = b1.x, x3 = a2.x, x4 = b2.x;
	double y1 = a1.y, y2 = b1.y, y3 = a2.y, y4 = b2.y;
	double x = (y3 - y1 + x1*(y2 - y1) / (x2 - x1) - x3*(y4 - y3) / (x4 - x3)) / ((y2 -
		y1) / (x2 - x1) - (y4 - y3) / (x4 - x3));
	return x;
}
void work(Point a, Point b) {
	b.y -= 1;
	for (int i = 0; i<n; i++) {
		Point p, q1, q2;
		p.x = point[i].x;
		p.y = a.y - (b.y - a.y) / (b.x - a.x)*(a.x - p.x);
		if ((p.y + eps<point[i].y&&p.y - eps>point[i].y - 1) ||
			abs(p.y - point[i].y)<eps || abs(p.y - point[i].y + 1)<eps)
			continue;
		if (i == 0) return;
		if (p.y - eps>point[i].y)
			ans = max(ans, intersect(a, b, point[i - 1], point[i]));
		else {
			q1 = point[i - 1];
			q1.y -= 1;
			q2 = point[i];
			q2.y -= 1;
			ans = max(ans, intersect(a, b, q1, q2));
		}
		return;
	}
	ok = true;
}
int main() {
	while (scanf("%d", &n), n) {
		for (int i = 0; i<n; i++)
			scanf("%lf%lf", &point[i].x, &point[i].y);
		ans = point[0].x;
		ok = false;
		for (int i = 0; i<n; i++)
			for (int j = 0; j<n; j++)
				if (i != j&&!ok)
					work(point[i], point[j]);
		if (ok)
			printf("Through all the pipe.\n");
		else
			printf("%.2f\n", ans);
	}
	return 0;
}
文章结束了，但我们的故事还在继续
坚持原创技术分享，您的支持将鼓励我继续创作！