7.20-stl专项训练题解

发表于 | 分类于 ， | 热度 ℃
字数统计: 6,249 | 阅读时长 ≈ 27

问题A

问题A同问题B，具体方法在问题B中介绍，此处仅贴代码

输入

首行输入t，代表t组测试样例

对于每一行，输入四个整数a，b，c，d

输出

对于每组样例，输出一个整数表示答案

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include<iostream>
#include<cstring>
#define ll long long
using namespace std;
const int maxn = 9;
ll a[4], sum[4] = { 0 };
ll dp[maxn * 4][maxn * 4];
//打表，递推公式C(a,b) = C(a,b-1)+C(a-1,b-1)
void init() {
	dp[0][0] = 0;
	for (int i = 1; i < 4 * maxn; i++) {
		dp[i][0] = 1;
		for (int j = 1; j < i; j++) {
			dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];
		}
		dp[i][i] = 1;
	}
}
int main() {
    int t;
    cin>>t;
    while(t--){
	init();//打表
	ll ans = 1;
	//这一步可要可不要，其实就是将a,a+b,a+b+c,a+b+c+d存进sum里
	for (int i = 0; i < 4; i++) {
		!i ? sum[i] = 0 : sum[i] = sum[i - 1];
		cin >> a[i];
		sum[i] += a[i];
		if (a[i] > sum[i] - a[i]) a[i] = sum[i] - a[i];
	}
	//将对应3组排列组合相乘，及C(b,a+b)C(c,a+b+c)C(d,a+b+c+d)
	for (int i = 1; i < 4; i++) {
		ans *= dp[sum[i]][a[i]];
	}
	cout << ans << endl;}
	return 0;
}

问题 B: yoyo思维题(困难)

问题A同问题B

提交: 4 解决: 2
[提交][状态][讨论版][命题人:qianyouyou][Edit] [TestData)]

题目描述

小琳，小花，小薇，yoyo，他们每个人手上有一堆牌，牌的张数分别为x1，x2，x3，x4，每张牌都不一样。现有n名同学，n=x1+x2+x3+x4。每名同学均需要一张牌，于是他们按顺序每人随机到四个人那里拿取牌顶的一张牌，最后一个人刚好拿到剩下的最后一张牌。排队拿牌的同学的顺序是固定的，选择拿谁的牌是不确定的。假如发牌的人手上的牌发完了，则要拿牌的同学会选择其他发牌的人。请问有多少种取法取走所有的牌。

输入

首行输入t，代表t组测试样例

对于每一行，输入四个整数a，b，c，d，输入为均不超过500的正整数

输出

对于每组样例，输出一个整数表示答案，答案对10^9+7取模

样例输入

1
2
1
5 4 2 3

样例输出

1
2522520

提示

本题作为思维题，并未用到stl，仅锻炼一下大家解决问题的能力。用到的数学知识相对多一点。

题解

题目大致可以理解为4堆牌a,b,c,d，每次从一堆牌里拿出牌顶的一张牌，问共有多少种拿法。其实我们可以一堆一堆的分析，假设只有一堆a时只有1种拿法，那两堆a,b时我们可以认为是从a个牌中插入b张牌，用数学表达式就是C(b,a+b);那么三堆的话我们可以把前两堆看成一堆，那么表达式就是C(c,a+b+c)，这是我们需要与前两堆的组成方法相乘，就是C(b,a+b)C(c,a+b+c)。4堆的话就是C(b,a+b)C(c,a+b+c)C(d,a+b+c+d)。所以答案就是C(a,a)C(b,a+b)C(c,a+b+c)C(d,a+b+c+d)。此外，有一公式C(a,b) = C(a,b-1)+C(a-1,b-1)，所以我们用数组来代替C(m,n)操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include<iostream>
#include<cstring>
#define ll long long
using namespace std;
const int maxn = 501;
const ll mod = 1000000007;
ll a[4], sum[4] = { 0 };
ll dp[maxn * 4][maxn * 4];
//打表，递推公式C(a,b) = C(a,b-1)+C(a-1,b-1)
void init() {
	dp[0][0] = 0;
	for (int i = 1; i < 4 * maxn; i++) {
		dp[i][0] = 1;
		for (int j = 1; j < i; j++) {
			dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];
			dp[i][j] %= mod;
		}
		dp[i][i] = 1;
	}
}
int main() {
    int t;
    cin>>t;
    while(t--){
	init();//打表
	ll ans = 1;
	//这一步可要可不要，其实就是将a,a+b,a+b+c,a+b+c+d存进sum里
	for (int i = 0; i < 4; i++) {
		!i ? sum[i] = 0 : sum[i] = sum[i - 1];
		cin >> a[i];
		sum[i] += a[i];
		if (a[i] > sum[i] - a[i]) a[i] = sum[i] - a[i];
	}
	//将对应3组排列组合相乘，及C(b,a+b)C(c,a+b+c)C(d,a+b+c+d)
	for (int i = 1; i < 4; i++) {
		ans *= dp[sum[i]][a[i]];
		ans %= mod;
	}
	cout << ans << endl;}
	return 0;
}

问题 C: 悠派计算器

提交: 4 解决: 1
[提交][状态][讨论版][命题人:qianyouyou][Edit][TestData)]

题目描述

yoyo的小老弟小渣渣灰特别懒，兴趣爱好并不多，就睡觉一个。为了多睡会儿懒觉，他把数学老师布置的作业全部推给yoyo计算。yoyo很头疼，于是请你帮他写一个计算器帮忙计算。现有多个数学表达式，请你写一个计算器算出结果，表达式只包含’+’’-‘’*’’/‘’%’’(‘’)’操作，其中表达式中’-‘作为减运算符，不会作为负号出现，此外’/‘为整除运算符，’%’为取余运算符。表达式保证合法。

输入

输入第一行t，表示共有t行测试用例，接下来t行每一行均为一个合法的数学表达式。保证每个数在[09999]范围内，保证计算过程中不会出现超范围情况。（注：没有空格）

输出

输出计算结果

样例输入

1
2
3
4
5
6
7
8
7
0*1
5%6
1-2*(3+4*5%6)+7/8-9*10%11*12
(1+2*3)
1-(100%5)
(3+2*5)/(5)
(11-11)+(33)*64-11

样例输出

1
2
3
4
5
6
7
0
5
-135
7
1
2
2101

提示

数据很水，不用考虑long long或取余等情况。

题解

逆波兰表达式是一种十分有用的表达式，它将复杂表达式转换为可以依靠简单的操作得到计算结果的表达式。例如(a+b)(c+d)转换为ab+cd+

如果当前字符为变量或者为数字，则压栈，如果是运算符，则将栈顶两个元素弹出作相应运算，结果再入栈，最后当表达式扫描完后，栈里的就是结果。

例如(a+b)(c+d)转换为ab+cd+ 计算机在计算普通表达式时，要对运算优先级用递归进行判断，对于更为复杂的表达式会使计算机运算效率变低甚至崩溃。而逆波兰表达式只需要进行简单的入栈出栈操作就可以完成任何普通表达式的运算。

普通表达式——>逆波兰表达式

(1)a+b——>a b +

(2)a+(b-c)——>a b c - +

(3)a+(b-c)d——>a b c - d +

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include<bits/stdc++.h>
using namespace std;
const int maxn = 100007;
map<char,int>Pri;//其实可以不必用map，只是为了方便大家理解map而多添加的一步
stack<int>num;
stack<char>Ope;
char str[maxn];
//初始化
void init(){
    Pri['+'] = Pri['-'] = 1;
    Pri['*'] = Pri['/'] = Pri['%'] = Pri['('] = Pri[')'] = 2;
    while(!num.empty())
        num.pop();
    while(!Ope.empty())
        Ope.pop();
}
//基本运算操作
void operation_1(int &a,int &b, char c){
    if(c == '+')
        a += b;
    else if(c == '-')
        a = b-a;
    else if(c == '*')
        a *= b;
    else if(c == '/')
        a = b/a;
    else if(c == '%')
        a = b%a;
}
//遇到+或者)时执行的操作
void operation_2(){
    char ch = Ope.top();
        while(ch != '('&&!Ope.empty()){
            Ope.pop();
            int a = num.top();
            num.pop();
            int b = num.top();
            num.pop();
            operation_1(a,b,ch);
            num.push(a);
            if(!Ope.empty())
                ch = Ope.top();
        }
        if(!Ope.empty()&&Ope.top() == '(')
            Ope.pop();
}
int main(){
    int t;
    cin>>t;getchar();
    while(t--){
        cin.getline(str,maxn);
        stringstream s(str);
        init();
        char tmp;
        while(s >> tmp){
        	//遇到数字字符时，需要判断下一位是否依旧是数字，是的话需要合并
            if(tmp >= '0' && tmp <= '9'){
                int t = 0;
                do{
                    if(Pri[tmp]){
                        break;
                    }
                    t *= 10;
                    t += tmp - '0';
                }while(s >> tmp);
                num.push(t);
            }
            //遇到')'时
            if(tmp == ')'){
                operation_2();
            }
            //遇到'+' ‘-’时
            else if(Pri[tmp]==1){
                if(!Ope.empty()&&Ope.top()!='('){
                    operation_2();
                }
                Ope.push(tmp);
            }
            else if(Pri[tmp]){
                Ope.push(tmp);
            }
        }
        int ans = num.top();
        num.pop();
        while(!num.empty()&&!Ope.empty()){
            operation_1(ans,num.top(),Ope.top());
            Ope.pop();
            num.pop();
        }
        cout << ans << endl;
    }
    return  0;
}

问题 D: 留胡子

提交: 53 解决: 6
[提交][状态][讨论版][命题人:qianyouyou][Edit] [TestData)]

题目描述

众所周知，刘虎子同学爱留胡子，人送外号刘胡子。为了留一抹性感又忧郁的小胡子，刘虎子专门与yoyo合作研发了一套算法，俗称油胡子算法。油胡子算法原理很简单，要想获得油胡子，首先将胡子从左到右分为n撮胡子，第i撮胡子的平均长度为xi。现每次从n中选出最左边的相邻胡子长度之差的绝对值为1的两撮胡子，减掉较长的1撮胡子，减掉的那撮胡子可以认为从n撮胡子中删除，剩下n-1撮胡子待修剪，再将剩下的n-1撮胡子从左到右重新排列成相邻的数继续如此操作，直到没有两撮相邻差的绝对值为1的胡子为止。此时的胡子称为完美油胡子。请问刘虎子同学最多需要剪多少次才能得到自己心仪的性感小胡子。

输入

输入第一行为n，接下来一行n个数x1x2…xi…xn。

输出

输出最多执行次数。

样例输入

1
2
6
3 2 3 1 0 1

样例输出

1
5

题解

用栈来维护每次合并完的数，每入栈一个数以后栈顶和次栈顶比较，如果可以合并就合并为新的栈顶，并且再次与次栈顶比较直至无法合并，在合并过程中统计次数即可。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <iostream>
#include <stack>
using namespace std;
int n,x;
int ans=0;     //最大操作次数
stack<int> st;
int main()
{
	int i;
	cin>>n;
	for(i=0;i<n;i++)
	{
		cin>>x;
		//将x与当前栈顶元素st.top()比较，若栈不空且st.top()比x大1，则合并一次(此时即当前栈顶元素出栈)
		//然后x与次栈顶比较，以此类推，直到不满足栈不空且st.top()比x大1
		while(!st.empty() && st.top()-x==1)
		{
			st.pop();
			ans++;
		}
		//若栈不空且x比st.top()大1，则合并一次
		//(此时即x"出栈"，也就是忽略此x继续看下一个输入的x 但栈不发生任何变化)
		if(!st.empty() && x-st.top()==1)
			ans++;
		//其他情况(x为第一个元素或不满足上述两种情况)：将x入栈
		else
			st.push(x);
	}
	cout<<ans<<endl;
	return 0;
}

问题 E: 卜卦

提交: 1 解决: 1
[提交][状态][讨论版][命题人:qianyouyou][Edit] [TestData)]

题目描述

赵神是一个特别特别闷骚的人。别看他平日表现很高冷，其实他一直暗恋着自己的小迷妹小花花，一日不见兮，思之如狂。马上快七夕了，赵神想卜一卦算一下他的爱情幸运数，于是他找到了yoyo半仙替他卜卦。yoyo半仙需要赵神的3个幸运数字以及小花花的3个幸运数字方可进行卜卦。已知赵神的3个幸运数字是’5’’2’’0’而小花花的幸运数字是abc，(保证由5，2，0，a，b，c，这6个数各不相同，且abc均为30以内的素数)。卜卦规则如下：
由{520abc}组成的6个各不相同数中选取最小的3个数作为加数，其余最大的3个数作为基数。每一个数若加上加数仅能被基数整除，其他素数均不能整除，则该数称为幸运数。其中第1314个幸运数为爱情幸运数。
现在你刚好知道小花花的幸运数，请你帮yoyo完成卜卦吧。PS：顺利完成任务后则会收获赵神珍藏版kiss一枚。

输入

首行输入t，代表t组测试样例

接下来t行输入三个数abc。

输出

输出第1314个幸运值

样例输入

1
2
3
2
7 3 11
7 11 13

样例输出

1
2
29541015622
1775105893556

来源

题解

待写

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int fort = 1314;
ll coeff[6];
int cmp(ll a,ll b){
    return a > b;
}
int main(){
    int t;
    cin>>t;
    while(t--){
        cin>>coeff[0]>>coeff[1]>>coeff[2];
        coeff[3] = 5;
        coeff[4] = 2;
        coeff[5] = 0;
        sort(coeff,  coeff + 6, cmp);
        priority_queue<ll, vector<ll>, greater<ll> > pq;
        set<ll>s;
        set<ll>ans;
        pq.push(1);
        s.insert(1);
        for(int i = 0;;i++){
            ll x = pq.top();
            pq.pop();
            if(i){
                for(int k = 3;k < 6;k++){
                    ans.insert(x - coeff[k]);
                    if(ans.size()==fort)
                        break;
                }
                if(ans.size()==fort){
                    /*int ttt = 1;
                    for(set<ll>::iterator it = ans.begin();it!=ans.end();it++)
                        cout<<ttt++<<' '<<*it<<endl;*/
                    set<ll>::reverse_iterator it = ans.rbegin();
                    cout<<*it<<endl;
                    break;
                }
            }
            for(int j = 0;j<3;j++){
                ll x2=x*coeff[j];
                if(!s.count(x2)){
                    s.insert(x2);
                    pq.push(x2);
                }
            }
        }
    }
    return 0;
}

问题 F: 成绩互评

提交: 117 解决: 40
[提交][状态][讨论版][命题人:qianyouyou][Edit] [TestData)]

题目描述

学生互评作业的简单规则是这样定的：每个人的作业会被k个同学评审，得到k个成绩。系统需要去掉一个最高分和一个最低分，将剩下的分数取平均，就得到这个学生的最后成绩。本题就要求你编写这个互评系统的算分模块。

输入

输入第一行给出3个正整数N（3< N <= 104，学生总数）、k（3<= k <= 10，每份作业的评审数）、M（<= 20，需要输出的学生数）。随后N行，每行给出一份作业得到的k个评审成绩（在区间[0 100]内），其间以空格分隔。

输出

按非递减顺序输出最后得分最高的M个成绩，保留小数点后3位。分数间有1个空格，行首尾不得有多余空格。

样例输入

1
2
3
4
5
6
7
6 5 3
88 90 85 99 60
67 60 80 76 70
90 93 96 99 99
78 65 77 70 72
88 88 88 88 88
55 55 55 55 55

样例输出

1
87.667 88.000 96.000

题解

total数组保存各个同学的平均分，v数组保存每次接收得到的分数，排序后取前m名，按递增输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include<iostream>
#include<algorithm>
#include<vector>
#include<cstdio>
using namespace std;
int cmp(double a, double b) {
	return a > b;
}
int main() {
	int N, K, M;
	while (cin >> N >> K >> M) {
		vector<double>v(K);
		vector<double>v2(N);
		for (int i = 0; i < N; i++) {
			double sum = 0;
			for (int j = 0; j < K; j++) {
				cin >> v[j];
				sum += v[j];
			}
			sort(v.begin(), v.end(), cmp);
			sum -= v[0] + v[K - 1];
			sum /= K - 2;
			v2[i] = sum;
		}
		sort(v2.begin(), v2.end(), cmp);
		for (int i = M - 1; i > 0; i--)
			printf("%.3lf ", v2[i]);
		printf("%.3lf\n", v2[0]);
	}
	return 0;
}

问题 G: 列车

提交: 18 解决: 10
[提交][状态][讨论版][命题人:qianyouyou][Edit] [TestData)]

题目描述

火车站的列车调度铁轨的结构如下图所示。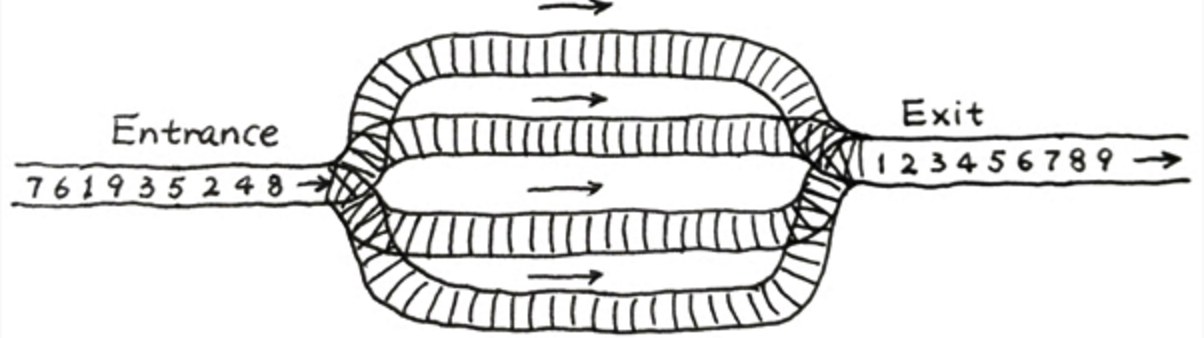
imgtle=”” align=”” />

两端分别是一条入口（Entrance）轨道和一条出口（Exit）轨道，它们之间有N条平行的轨道。每趟列车从入口可以选择任意一条轨道进入，最后从出口离开。在图中有9趟列车，在入口处按照{8，4，2，5，3，9，1，6，7}的顺序排队等待进入。如果要求它们必须按序号递减的顺序从出口离开，则至少需要多少条平行铁轨用于调度？

输入

输入第一行给出一个整数N (2 <= N <= 105)，下一行给出从1到N的整数序号的一个重排列。数字间以空格分隔。

输出

在一行中输出可以将输入的列车按序号递减的顺序调离所需要的最少的铁轨条数。

样例输入

1
2
9
8 4 2 5 3 9 1 6 7

样例输出

1
4

题解

必须要车号大的先出，小的后出。所以列车排队的每一队必须是从大到小排列（从右往左看），才能保证开出去的车也是从大到小的。 对于每一个想要进入并列铁轨的车，如果车号大于每一队的队尾的车号，说明不能进入已经有的队伍，必须进入新的铁轨 否则，选择一个最接近它车号的尾部车号的队伍进入 其实无需保存每一个并行队列的所有值，只需要保存当前队伍的车尾（就是每一列最左边 即 每一列的最小值）即可 因为每一次都是需要排序比较大小的，所以用set自动排序 首先把set里面放入一个0值。每一次set的最后一个值s.rbegin()都是当前所有队列队尾的最大值. 如果当前想要进入排队队伍的t值比集合里面最大值小，就移除第一个比他大的值，然后把t插入集合中。表示的是将t值插入了最接近它车号的队伍的队尾 否则就直接插入进去t值。作为新的队伍。s.upper_bound(t)返回的是第一个大于t的迭代器的位置 在前面加星号表示取这个位置的值 所以s.erase(*(s.upper_bound(t)));表示删除当前这个刚好大于t的位置处的值 因为一开始插入了一个没有的0，所以最后输出是s.size()-1。** 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <iostream>
#include <set>
using namespace std;
int main() {
    int n, t;
    cin >> n;
    set<int> s;
    s.insert(0);
    for(int i = 0; i < n; i++) {
        cin >> t;
        if(t < *s.rbegin()) {
            s.erase(*(s.upper_bound(t)));
        }
        s.insert(t);
    }
    cout << s.size() - 1;
    return 0;
}

问题 H: 新浪关注

提交: 24 解决: 14
[提交][状态][讨论版][命题人:qianyouyou][Edit] [TestData)]

题目描述

新浪微博上有个“悄悄关注”，一个用户悄悄关注的人，不出现在这个用户的关注列表上，但系统会推送其悄悄关注的人发表的微博给该用户。现在我们来做一回网络侦探，根据某人的关注列表和其对其他用户的点赞情况，扒出有可能被其悄悄关注的人。

输入

输入首先在第一行给出某用户的关注列表，格式如下：

人数N 用户1 用户2 …… 用户N

其中N是不超过5000的正整数，每个“用户i”（i=1 … N）是被其关注的用户的ID，是长度为4位的由数字和英文字母组成的字符串，各项间以空格分隔。

之后给出该用户点赞的信息：首先给出一个不超过10000的正整数M，随后M行，每行给出一个被其点赞的用户ID和对该用户的点赞次数（不超过1000），以空格分隔。注意：用户ID是一个用户的唯一身份标识。题目保证在关注列表中没有重复用户，在点赞信息中也没有重复用户。

输出

我们认为被该用户点赞次数大于其点赞平均数、且不在其关注列表上的人，很可能是其悄悄关注的人。根据这个假设，请你按用户ID字母序的升序输出可能是其悄悄关注的人，每行1个ID。如果其实并没有这样的人，则输出“Bing Mei You”。

样例输入

1
2
3
4
5
6
7
8
9
10
10 GAO3 Magi Zha1 Sen1 Quan FaMK LSum Eins FatM LLao
8
Magi 50
Pota 30
LLao 3
Ammy 48
Dave 15
GAO3 31
Zoro 1
Cath 60

样例输出

1
2
3
Ammy
Cath
Pota

题解

将关注的人存储在集合set里，将点赞的人和点赞的次数存储在map中，并统计点赞的平均次数sum / M，遍历map，如果map的值大于平均次数，且在set中找不到该用户名，就输出当前用户名（因为map中的键是已经按照字典序排序过的，所以直接输出就可以），并用flag标记是否有过输出，如果从始至终没有输出，说明没有悄悄关注的人，就输出Bing Mei You 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<iostream>
#include<set>
#include<map>
#include<string>
using namespace std;
int main(){
	int m, n;
	while (cin >> n) {
		set<string>id;
		while (n--) {
			string name;
			cin >> name;
			id.insert(name);
		}
		cin >> m;
		map<string, int>mm;
		int sum = 0;
		for (int i = 0; i < m; i++) {
			int cnt;
			string str;
			cin >> str >> cnt;
			mm[str] = cnt;
			sum += cnt;
		}
		sum /= m;
		int flag = 0;
		for (auto it : mm) {
			if (it.second > sum&&id.find(it.first) == id.end()) {
				cout << it.first << endl;
				flag = 1;
			}
		}
		if (!flag)
			cout << "Bing Mei You" << endl;
	}
	return 0;
}

问题 I: 礼物

提交: 94 解决: 44
[提交][状态][讨论版][命题人:qianyouyou][Edit] [TestData)]

题目描述

四月一日快到了，Vayko想了个愚人的好办法——送礼物。嘿嘿，不要想的太好，这礼物可没那么简单，Vayko为了愚人，准备了一堆盒子，其中有一个盒子里面装了礼物。盒子里面可以再放零个或者多个盒子。假设放礼物的盒子里不再放其他盒子。
用()表示一个盒子，B表示礼物，Vayko想让你帮她算出愚人指数，即最少需要拆多少个盒子才能拿到礼物。

输入

本题目包含多组测试，请处理到文件结束。
每组测试包含一个长度不大于1000只包含’(‘’)’和’B’三种字符的字符串，代表Vayko设计的礼物透视图。
你可以假设，每个透视图画的都是合法的。

输出

对于每组测试，请在一行里面输出愚人指数。

样例输入

1
2
((((B)()))())
(B)

样例输出

1
2
4
1

题解

看上去像是编译原理的文法识别，要用到栈，其实不是，只要看准备上面红色的字，就知道，只有三种字符()B，且待处理的串为合法的文法，所以要知道包装盒的个数，只要知道B前面有多少(字符，但可能有(()B)这种情况，B前面有)，但因为合法，所以可以在B之前的找到(与)相匹配，就剔除掉了，所以盒子的个数就是B之前的串中(的个数减去)的个数。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include<iostream>
#include<string>
using namespace std;
int main() {
	string str;
	while (cin >> str) {
		int sco = 0;
		for (int i = 0; i < str.length(); i++) {
			if (str[i] == '(')
				sco++;
			else if (str[i] == ')')
				sco--;
			else if (str[i] == 'B')
				break;
		}
		cout << sco << endl;
	}
	return 0;
}

问题 J: Sunscreen

题意：有C头奶牛要去沐光浴，太阳光太强烈会晒坏皮肤，太弱又会没效果。每头牛都有一个太阳光适宜的范围经行沐光浴，分别给出minspf_i和maxspf_i。 有L种防晒霜，每种防晒霜可以把所受阳光固定于一个值spf_i，每种有cover_i瓶。 问最多会有几头牛得到合适的光晒强度？

题解：贪心策略，在满足minspf的条件下，尽量将spf的防晒霜涂到maxspf小的奶牛身上，因为maxspf大的奶牛有更多的选择。这里就需要一个优先队列来储存满足minspf的奶牛的maxspf的值。 具体解题步骤如下：

1.将奶牛按照minspf升序排列，将防晒霜按照spf升序排列。

2.枚举防晒霜，将minspf<=spf的奶牛的maxspf存到优先队列中，然后值小的先出队列，看是否满足maxspf>=spf，更新记录值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include<iostream>
#include<algorithm>
#include<queue>
#include<vector>
using namespace std;
const int MAXN = 12505;
struct spf {
	int max;
	int min;
	friend bool operator < (spf a, spf b) {
		return a.min < b.min;
	}
}cow[MAXN], bot[MAXN];
struct cmp {
	bool operator()(const int a, const int b)const {
		return a > b;
	}
};
int main() {
	int C, L, i;
	priority_queue<int, vector<int>, cmp>pq;
	while (cin >> C >> L) {
		for (i = 0; i < C; i++)
			cin >> cow[i].min >> cow[i].max;
		for (i = 0; i < L;i++)
			cin >> bot[i].min >> bot[i].max;
		sort(cow, cow + C);
		sort(bot, bot + L);
		int cur = 0, ans = 0;
		for(int i=0;i<L;i++){
			while(cur < C&&cow[cur].min <= bot[i].min) { 
				pq.push(cow[cur].max); 
				cur++; 
			}
			while(!pq.empty()&&bot[i].max) { 
				int maxSPF = pq.top(); 
				pq.pop();
				if(maxSPF >= bot[i].min){
					ans++; 
					bot[i].max--;
				}
			} 
		}
		cout<<ans<<endl;
	}
	return 0;
}
文章结束了，但我们的故事还在继续
坚持原创技术分享，您的支持将鼓励我继续创作！