图的连通性

连通图

所谓连通性，直观的讲，就是“连成一片”。

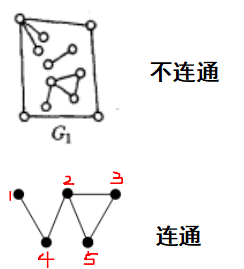
我们发现，按照上面的划分方法，我们可以把G1分为三部分，因此，G1是不连通的，但是，这三个部分，我们把它们叫做图G1的三个连通分量。

定义

无向图G中，如果任意两顶点u和v，都能找到从一条u到v的路径。称无向图G是连通的。

当G为有向图时，若G中存在一条以 u为起点 v为终点的有向路P，则称从 u到 v是可达的。

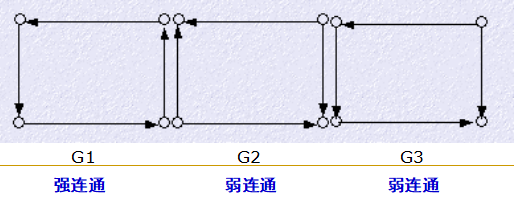
如果G的任何两个顶点都是相互可达的，则称图G是强连通的；如果G的有向边被看作无向边时是连通的，则称有向图G是弱连通的。

连通分量

所谓连通分量，指的是图中的极大连通子图。

有了连通分量的概念，我们可以对图的连通性换言之为：如果图G中只有唯一一个连通分量，那么G是连通的，我们称G为连通图。

强连通

无向图连通性

在对无向图进行遍历时，对于连通图，仅需从图中任一顶点出发，进行深度优先遍历或广度优先遍历，便可访问到图中所有顶点；对于非连通图，则需从多个顶点出发进行遍历，而每次从一个新的起点出发进行遍历得到的顶点访问序列恰好是一个连通分量中的顶点集。

方法

对无向图的连通性判定，一般我们采用搜索的方法，这里我们首先要提到应用非常广泛的深度优先搜索算法DFS，DFS在图论算法中有非常重要的地位。

例子

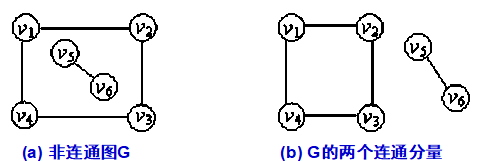
对下图( a ) 所示无向图进行深度优先遍历，需分别从顶点 v 1 和 v 5 出发调用两次 DFS（或 BFS），得到的顶点序列分别为： v 1 v 2 v 3 v 4 和 v 5 v 6 。这两个顶点集分别加上所有依附于这些顶点的边，便构成了非连通图 G 的两个连通分量，如下图 ( b ) 所示。

代码

因此，要想判定一个无向图是否为连通图，或有几个连通分量，可以设置一个计数器 count ，初始时取值为 0 ，每调用一次遍历算法，就给 count 增 1 。这样，当整个遍历算法结束时，依据 count 的值，就可确定图的连通性了。算法用伪代码描述如下：

无向图连通分支
//无向图连通分支，dfs邻接阵形式，o（n^2）
//返回分支数，id返回1..分支数的值
//传入图的大小n和邻接阵mat，不相邻点边权0
#define MAXN 100 
void floodfill(int n,int mat[][MAXN],int* id,int now,int tag){
int i; 
for (id[now]=tag,i=0;i<n;i++) 
	if (!id[i]&&mat[now][i]) 
		floodfill(n,mat,id,i,tag); 
}
int find_components(int n,int mat[][MAXN],int* id){ 
	int count,i; 
	for (i=0;i<n;id[i++]=0); 
		for (count=i=0;i<n;i++) 
			if (!id[i]) 
				floodfill(n,mat,id,i,++count); 
	return count; 
}

有向图连通性

假设，我们把一张有向图的所有边看做无向的，然后对转化后的无向图进行一次DFS，是不是就可以判断无向图的连通性呢？显然可以。

对于采用邻接矩阵表示的有向图G=<E，V>，如果存在一条边e(u,v),那么在矩阵中e(u,v)>0，我们令e(v,u)=e(u,v)，这样就可以将一条有向边变成无向边。

之后，对于这个转化后的矩阵进行一次DFS，这样既可以判断有向图是否连通。

需要注意的是，一般情况下，我们在题目中应用到得不是简单的有向图是否连通，而是：求有向图的强连通分量。

有向图的强连通分量

有向图G的极大强连通子图称为G的强连通分量(SCC)。

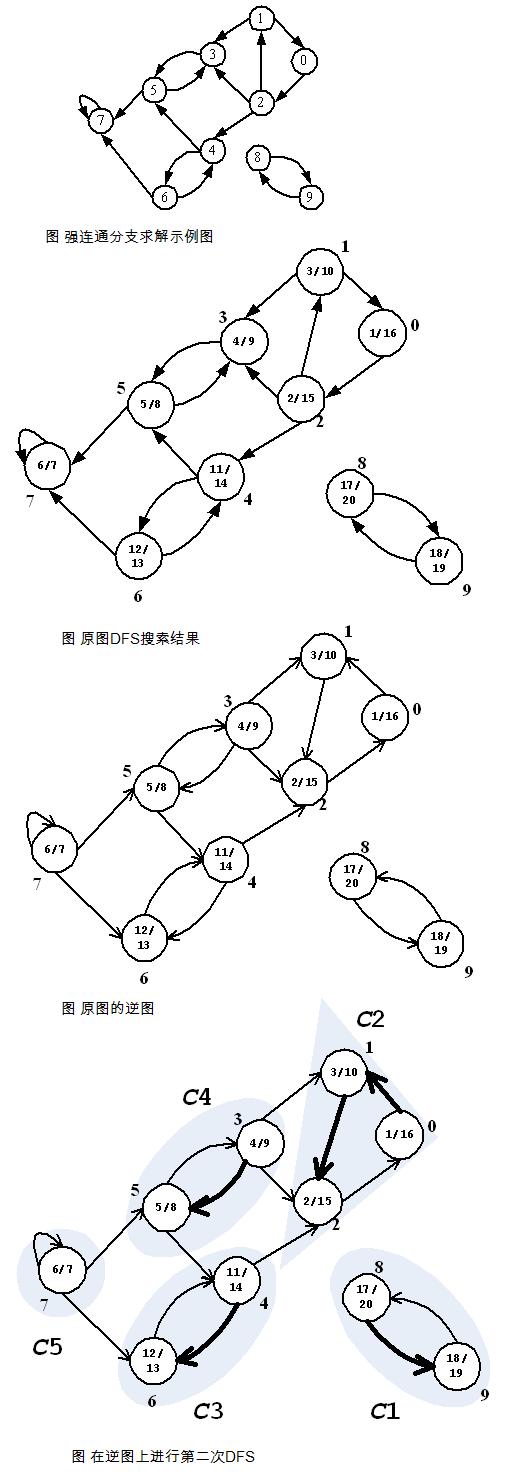
下图中，子图{1,2,3,4}为一个强连通分量，因为顶点 1,2,3,4 两两可达。{5},{6}也分别是两个强连通分量。

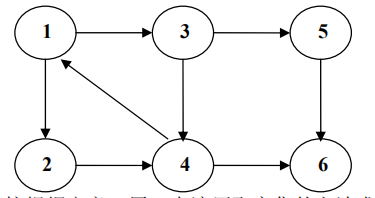
直接根据定义，用双向遍历取交集的方法求强连通分量，时间复杂度为 O(N^2+M)。
更好的方法是 Kosaraju 算法或和Tarjan 算法，两者的时间复杂度都是 O(N+M)。还有Gabow算法不介绍。

Kosaraju 算法

Kosaraju算法的解释和实现都比较简单，为了找到强连通分支，首先对图G运行DFS，计算出各顶点完成搜索的时间f；然后计算图的逆图GT，对逆图也进行DFS搜索，但是这里搜索时顶点的访问次序不是按照顶点标号的大小，而是按照各顶点f值由大到小的顺序；逆图DFS所得到的森林即对应连通区域。具体流程如图(1~4)。

上面我们提及原图G的逆图GT，其定义为GT=(V, ET)，ET={(u, v):(v, u)∈E}}。也就是说GT是由G中的边反向所组成的，通常也称之为图G的转置。在这里值得一提的是，逆图GT和原图G有着完全相同的连通分支，也就说，如果顶点s和t在G中是互达的，当且仅当s和t在GT中也是互达的。

在这里顺便提一下在调用dfs的过程中，几种添加顶点到集合的顺序。一共有四种顺序：

Pre-Order，在递归调用dfs之前将当前顶点添加到queue中
Reverse Pre-Order，在递归调用dfs之前将当前顶点添加到stack中
Post-Order，在递归调用dfs之后将当前顶点添加到queue中
Reverse Post-Order，在递归调用dfs之后将当前顶点添加到stack中

最后一种的用途最广，至少目前看来是这样，比如步骤2-a以及拓扑排序中，都是利用的Reverse Post-Order来获取顶点集合。

步骤

(1)对G执行深度优先搜索，求出每个顶点的后序遍历顺序号postOrder。

(2)反转有向图G中的边，构造一个新的有向图G*。

(3)由最高的postOrder编号开始，对G*执行深度优先搜索。如果深度优先搜索未达到所有顶点，由未访问的最高postOrder编号的顶点开始，继续深度优先搜索。

(4)步骤三所产生的森林中的每一棵树，对应于一个强连通分支。

代码

#define maxN 1024
int marked[maxN];//用于记录某个点是否被访问过，0为没有被临幸过，1为被临幸过
int id[maxN];//记录每个点所属的连通分量
int count;//记录连通分量总数目
void kosaraju(graph *g){
    int i;
    memset(marked,0,sizeof(marked));
    memset(id,0,sizeof(id));
    count=0;
    for(i=0;i<g->V;i++){//之所以这里用循环就是因为g指向的无向图可能不是一个连通图，而是由多个连同分量组成
        if(!marked[i]){dfs(g,i); count++;}
    }
}
 
 
void dfs(graph *g,int v){
    graphNode *t;
    marked[v]=1;
    id[v]=count;
    t=g->adjlist[v].next;//t指向v的邻接点
    while(t){
        if(!marked[t->key]){dfs(g,t->key);}//这里是重点，就是你发现v到t->key有路径就把它算到跟自己在一个连通分量里了，这里有一个隐性前提，就是你提前知道t->key一定可以到v，所以你发现v可以到t->key的时候，你毫不犹豫把它算为跟自己一伙儿的了。Korasaju算法不同书上有不同的表述，区别是先遍历图g还是先遍历图g的逆向图，这只是顺序的区别。我把我看得版本完整说一下：（1）先DFS遍历图g的逆向图，记录遍历的逆后序。（什么叫逆后序？逆后序就是DFS时后序的逆序，注意逆后序不一定为DFS的前序。DFS前序为，访问某个顶点前，把它push进队列。DFS后序为访问完某个顶点后才把它push进队列。而DFS逆后序为访问完某个顶点后把它push进一个栈中。当DFS遍历完整个图后，后序队列的输出与逆后序栈的输出正好相反。）（2）然后按着图g逆向图的DFS遍历的逆后序序列遍历图g求所有的强连通分量，这一步的过程跟无向图求所有连通分量的算法一模一样！按着这里说的遍历顺序重复无向图求所有连通分量的步骤求出来的就是有向图的所有强连通分量，为什么呢？因为我们完成第一步后，按着第一步得到的逆后序要对有向图g进行DFS遍历的前一刻，前面这段过程就相当于我们完成了对这幅有向图g一个加工，把它加工成了一个无向图！也就是说，这个加工实现了我注释开头提到的那个隐性前提。所以后面按着无向图求所有连通分量的步骤求出来的就是有向图g的所有强连通分量。举个例子，比如有向图3->5->4->3，它的逆向图为3->4->5->3（你最好在纸上画下，就是个三角循环图），从逆向图的顶点3开始DFS，得到的逆后续为3，4,5 。按着这个顺序对原图进行DFS，DFS(3)时遇到5，则5肯定跟3在一个强连通分量中（为什么？因为我们逆向图DFS(5)时肯定能到达3，这就是隐形前提。所以正向图DFS(3)遇到5时，我们毫不犹豫把它算到自己一个强连通分量中。）
        t=t->next;
    }
}

Tarjan 算法

Tarjan 算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。定义 DFN(u)为节点 u 搜索的次序编号(时间戳)，Low(u)为 u 或 u 的子树能够追溯到的最早的栈中节点的次序号。由定义可以得出

Low(u)=Min 
{ 
 DFN(u), 
 Low(v),(u,v)为树枝边，u为v的父节点
 DFN(v),(u,v)为指向栈中节点的后向边(非横叉边) 
}

当 DFN(u)=Low(u)时，以 u 为根的搜索子树上所有节点是一个强连通分量。
算法伪代码如下：

tarjan(u) 
{ 
	DFN[u]=Low[u]=++Index // 为节点u设定次序编号和Low初值
	Stack.push(u) // 将节点u压入栈中
	for each (u, v) in E // 枚举每一条边
		if (v is not visted) // 如果节点v未被访问过
			tarjan(v) // 继续向下找
			Low[u] = min(Low[u], Low[v]) 
		else if (v in S) // 如果节点v还在栈内
			Low[u] = min(Low[u], DFN[v]) 
	if (DFN[u] == Low[u]) // 如果节点u是强连通分量的根
 		repeat 
			v = S.pop // 将v退栈，为该强连通分量中一个顶点
 			print v 
		until (u== v) 
}

流程

从节点 1 开始 DFS ，把遍历到的节点加入栈中。搜索到节点 u=6 时，DFN[6]=LOW[6]，找到了一个强连通分量。退栈到 u=v 为止，{6}为一个强连通分量。

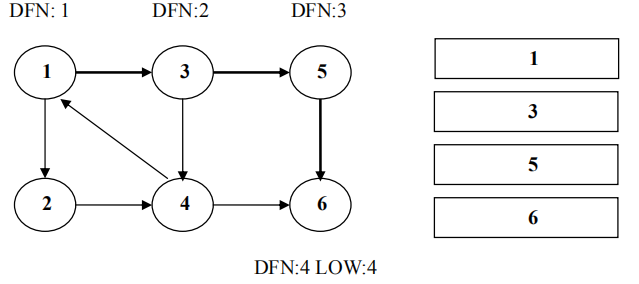
返回节点 5，发现 DFN[5]=LOW[5]，退栈后{5}为一个强连通分量。

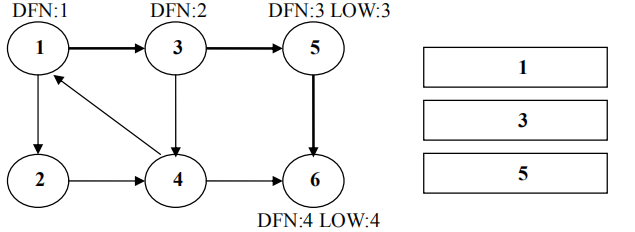
返回节点 3，继续搜索到节点 4，把 4 加入堆栈。发现节点 4 向节点 1 有后向边，节点 1 还在栈中，所以 LOW[4]=1。节点 6 已经出栈，(4,6)是横叉边，返回 3，(3,4)为树枝边，所以 LOW[3]=LOW[4]=1。

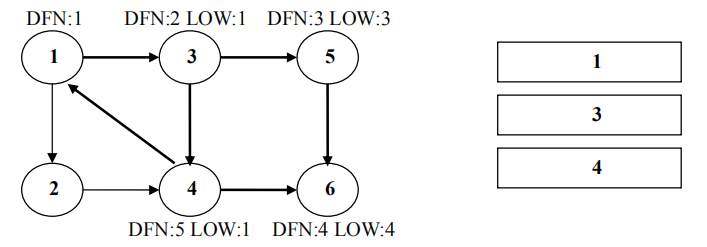
继续回到节点 1 ，最后访问节点 2 。访问边 (2,4) ， 4 还在栈中，所以LOW[2]=DFN[4]=5。返回 1 后，发现 DFN[1]=LOW[1]，把栈中节点全部取出，组成一个连通分量{1,3,4,2}。

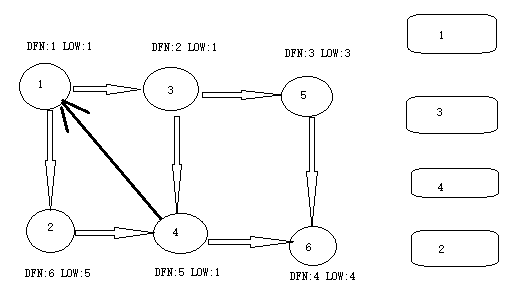
至此，算法结束。经过该算法，求出了图中全部的三个强连通分量{1,3,4,2},{5},{6}。可以发现，运行 Tarjan 算法的过程中，每个顶点都被访问了一次，且只进出了一次堆栈，每条边也只被访问了一次，所以该算法的时间复杂度为 O(N+M)。

代码

void tarjan(int i)
{
    int j;
    DFN[i]=LOW[i]=++Dindex;
    instack[i]=true;
    Stap[++Stop]==i;
    for (edge *e=V[i]; e; e=e->next)
    {
        j=e->t;
        if (!DFN[j])
        {
            tarjan(j);
            if (LOW[j]<LOW[i])
                LOW[i]=LOW[j];
        }
        else if (instack[j] && DFN[j]<LOW[i]
                )
            LOW[i]=DFN[j];
    }
    if (DFN[i]==LOW[i])
    {
        Bcnt++;
        do
        {
            j=Stap[Stop--];
            instack[j]=false;
            Belong[j]=Bcnt;
        }
        while (j!=i);
    }
}
void solve()
{
    int i;
    Stop=Bcnt=Dindex=0;
    memset(DFN,0,sizeof(DFN));
    for (i=1; i<=N; i++)
        if (!DFN[i])
            tarjan(i);
}

Gabow算法

这个算法其实就是Tarjan算法的变异体，我们观察一下，只是它用第二个堆栈来辅助求出强连通分量的根，而不是Tarjan算法里面的dfn[]和backn[]数组。那么，我们说一下如何使用第二个堆栈来辅助求出强连通分量的根。

我们使用类比方法，在Tarjan算法中，每次backn[i]的修改都是由于环的出现(不然，backn[i]的值不可能变小)，每次出现环，在这个环里面只剩下一个backnk[i]没有被改变(深度最低的那个)，或者全部被改变，因为那个深度最低的节点在另一个环内。那么Gabow算法中的第二堆栈变化就是删除构成环的节点，只剩深度最低的节点，或者全部删除，这个过程是通过出栈来实现，因为深度最低的那个顶点一定比前面的先访问，那么只要出栈一直到栈顶那个顶点的访问时间不大于深度最低的那个顶点。其中每个被弹出的节点属于同一个强连通分量。那有人会问：为什么弹出的都是同一个强连通分量？因为在这个节点访问之前，能够构成强连通分量的那些节点已经被弹出了，这个对Tarjan算法有了解的都应该清楚，那么Tarjan算法中的判断根我们用什么来代替呢？想想，其实就是看看第二个堆栈的顶元素是不是当前顶点就可以了。

现在，你应该明白其实Tarjan算法和Gabow算法其实是同一个思想的不同实现，但是，Gabow算法更精妙，时间更少(不用频繁更新backn[])。

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<stack>
using namespace std;
bool map[100][100];//记录图形
bool visited[100];//记录点是不是已经被访问过了
bool del[100];//记录点是不是已经删除了
int dfn[100];//记录点访问的次序
stack<int>s1,s2;
int dotn;
void init()
{
    int line;
    cin>>dotn>>line;
    for(int i=1;i<=line;i++)
    {
        int u,v;
        cin>>u>>v;
        map[u][v]=1;
    }
    memset(visited,0,sizeof(visited));
    memset(del,0,sizeof(del));
}
void dfs(int u,int &time)
{
    visited[u]=1;
    dfn[u]=++time;
    s1.push(u);
    s2.push(u);
    for(int i=1;i<=dotn;i++)
    {
        if(map[u][i])
        {
            if(!visited[i])
            {
                dfs(i,time);
            }
            else
            {
                if(!del[i])
                {
                    while(dfn[s2.top()]>dfn[i])s2.pop();//注意这个地方
                }
            }
        }
    }
    if(u==s2.top())
    {
        while(u!=s1.top())
        {
            cout<<s1.top()<<"   ";
            del[s1.top()]=1;
            s1.pop();
        }
        cout<<u<<endl;
        del[s1.top()]=1;
        s1.pop();
        s2.pop();
    }
}
void Gadow()
{
    init();
    int time=0;
    for(int i=1;i<=dotn;i++)
    {
        if(!visited[i])
        {
            dfs(i,time);
        }
    }
}
int main()
{
    freopen("in.txt","r",stdin);
    Gadow();
    return 0;
}

应用

强连通分支问题的最大应用就在于两个字：缩点！

所谓缩点，就是把图中属于同一个强连通分支中的点缩为一个点，这样，我们就得到了一个新的有向图，而且图中不存在回路。

POJ 1236 - Network of Schools（最小点基）

2-SAT

有向图缩点一个很大的应用，就是2-SAT问题(2判定性问题 )。

POJ 3678 - Katu Puzzle

POJ 3683 - Priest John’s Busiest Day

2-SAT

定义 1:

布尔变量 x，假如逻辑运算“或”和“与”分别用“∨”和“∧ ”来表示，﹁x表示 x 的非，布尔表达式是用算术运算符号连接起来的变量所构成的代数表达式。给定每个变量 x 的一个值 p(x)，可以像计算代数表达式一样计算布表达式的值。如果存在一个真值分配，使得布尔表达式的取值为真，则这个布尔表达式称为可适定性的，简称 SAT。

例如（x1∨x2）∧(﹁x1∨﹁x2) 这个布尔表达式，如果 p(x1)=真，p(x2)=假，则表达式的值为真，则这个表达式是适定性的。不是所有的布尔表达式都是可适定的。

例如x1∧﹁x2∧(﹁x1∨x2)，则不管 p(x1),p(x2)取何值，表达式都不可能为真，因此这个布尔表达式是不可适定的。

适定性问题的一般形式 X=｛x1,x2..,xn｝为一个有限的布尔变量集，包含 x1,x2，..,xn的“或”和“与”，运算的 m 个句子 C1,C2,..,Cm,布尔表达式 C1∧C2∧,..,∧Cm 是否可适定。

布尔表达式由用“与”连接起来的一些句子构成，则称这个表达式为“合取范式”。

定义 2:

对于给定的句子 C1,C2,..,Cm,如果 max{|Ci|}=k(1≦i≦m),则称此适定性问题为 k 适定性问题，简称 k-SAT。

当 k>2 时，k-SAT 是 NP 完全的，所以我们一般讨论2-SAT问题。

解题思路

下面我们从一道例题来认识 2-SAT 问题，并提出对一类 2-SAT 问题通用的解法。
Poi 0106 Peaceful Commission [和平委员会]

某国有 n 个党派，每个党派在议会中恰有 2 个代表。现在要成立和平委员会，该会满足：

每个党派在和平委员会中有且只有一个代表
如果某两个代表不和，则他们不能都属于委员会
代表的编号从 1 到 2n，编号为 2a-1、2a 的代表属于第 a 个党派

输入 n（党派数），m（不友好对数）及 m 对两两不和的代表编号
其中 1≤n≤8000，0≤m ≤20000
求和平委员会是否能创立。
若能，求一种构成方式。

例：

输入：

3 2

1 3

2 4

输出：

分析

原题可描述为：

有 n 个组，第 i 个组里有两个节点 Ai, Ai’ 。需要从每个组中选出一个。而某些点不可以同时选出（称之为不相容）。任务是保证选出的 n 个点都能两两相容。（在这里把 Ai,Ai’ 的定义稍稍放宽一些，它们同时表示属于同一个组的两个节点。也就是说，如果我们描述 Ai，那么描述这个组的另一个节点就可以用 Ai’）

初步构图

如果 Ai 与 Aj 不相容，那么如果选择了 Ai，必须选择 Aj ‘ ；同样，如果选择了 Aj，就必须选择 Ai ’ 。

Ai → AjAj → Ai

这样的两条边对称

我们从一个例子来看：

假设 4 个组，不和的代表为：1 和 4，2 和 3，7 和 3，那么构图：

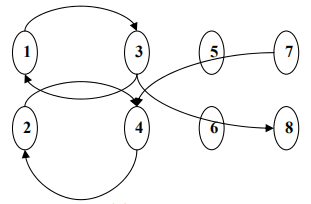
假设：

首先选 1
3 必须选，2 不可选
5、6 可以任选一个
8 必须选，4、7 不可选

矛盾的情况为：
存在 Ai，使得 Ai 既必须被选又不可选。
得到算法 1：
枚举每一对尚未确定的 Ai, Ai‘ ，任选 1 个，推导出相关的组，若不矛盾，则可选择；否则选选另 1 个，同样推导。若矛盾，问题必定无解。

此算法正确性简要说明：

由于 Ai,Ai’ 都是尚未确定的，它们不与之前的组相关联，前面的选择不会影响 Ai,Ai’ 。
算法的时间复杂度在最坏的情况下为 O(nm)。

在这个算法中，并没有很好的利用图中边的对称性
观察图（1）可以发现，1 和 3 构成一个环，这样 1 和 3 要么都被选中，要么都不选。2和 4 也同样如此。

在每个一个环里，任意一个点的选择代表将要选择此环里的每一个点。不妨把环收缩成一个子节点。新节点的选择表示选择这个节点所对应的环中的每一个节点。

对于原图中的每条边 Ai → Aj（设 Ai 属于环 Si，Aj 属于环 Sj）如果 Si≠Sj，则在新图中连边：

Si → Sj

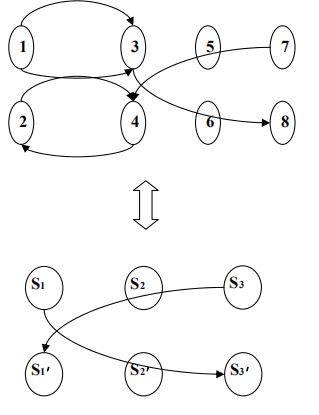
这样构造的有向无环图和原图是等价的，这样我们就可以用之前介绍过的强连通分量的算法把图转化成有向无环图，在这个基础上，如果存在一对 Ai, Ai’属于同一个环，则判无解，否则将采用拓扑排序，以自底向上的顺序进行推导，一定能找到可行解。

下面给出 2-SAT 问题中常用的建边方式：

2-SAT 中元素关系常见有以下 11 种

A[x]

NOT A[x]

A[x] AND A[y]

A[x] AND NOT A[y]

A[x] OR A[y]

A[x] OR NOT A[y]

NOT (A[x] AND A[y])

NOT (A[x] OR A[y])

A[x] XOR A[y]

NOT (A[x] XOR A[y])

A[x] XOR NOT A[y]

And 结果为 1：建边 ~x->y, ~y->x (两个数都为 1)
And 结果为 0：建边 y->~x , x->~y(两个数至少有一个为 0)
OR 结果为 1：建边 ~x->y , ~y->x(两个数至少有一个为 1)
OR 结果为 0：建边 x->~x , y->~y(两个数都为 0)
XOR 结果为 1：建边 x->~y , ~x->y , ~y->x , y -> ~x (两个数一个为 0，一个为 1)
XOR 结果为 0：建边 x->y , ~x->~y , y->x ~y->~x(两个数同为 1 或者同为 0)

对于一般判定是不是有解的情况，我们可以直接采用 tarjan 算法求强联通，然后缩点，如果 x 与~x 染色相同，说明无解，否则有解。有的时候，可能需要用二分++tarjan 算法

欧拉图

每个小点最后都会回到自己原来的位置上吗？注意，这些小点并不是沿着一个回路在运动，而是沿着三个交替出现的回路在运动。

答案是肯定的。 math 版上的 OmnipotentEntity 给出了一个简短的证明。假设某个地方的小点出发后永远不会回到原地。由于小点的运动规律是三步一个周期，因此每三步之后从此处出发的小点将会拥有完全相同的命运——永远不会回到原地。既然从这里出发的小点会不断地发生有去无回的情况，那么总有一个时候小点会被用光，此时就再也没有小点能从这里出发了。但这与我们看到的实际情况相矛盾：每个地方的小点都是用之不竭的。

熟悉群论的朋友会很快发现，这个结论几乎是显然的。小点的每一步运动都形成了一个置换，三个置换的复合本质上也还是一个置换，而这个置换的足够多次幂一定会变成单位置换。这意味着，不但每个点都能回到自己原来的位置，而且所有点能同时回到自己原来的位置（后者可能需要更长的时间）。事实上，有限群中的任意一个元素都有一个有限的阶，因而如果某类变换操作能构成一个有限群的话，不断地执行某一个操作，或者不断地循环执行某几个操作，最后总有一个时刻你会发现，一切又都重新变回了原样。拿出一副新的扑克牌，每次洗牌时都把牌分成两半并把它们完美地交叉在一起，那么不断这样洗下去之后，整副牌总会在某个时候重新变得有序。找一个复原好了的魔方，循环执行几个固定的操作，魔方很快就会被彻底打乱，但最终一定会奇迹般地再次复原。

欧拉图（E问题）

起源：

欧拉回路问题是图论中最古老的问题之一。它诞生于十八世纪的欧洲古城哥尼斯堡。普瑞格尔河流经这座城市，人们在两岸以及河中间的两个小岛之间建了七座桥（如图1）。

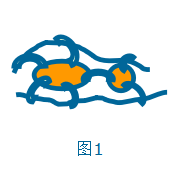
于是产生了这样一个问题：是否可以找到一种方案，使得人们从自己家里出发，不重复地走遍每一座桥，然后回到家中？这个问题如果用数学语言来描述，就是在图2中找出一条回路，使得它不重复地经过每一条边。这便是著名的“哥尼斯堡七桥问题”。

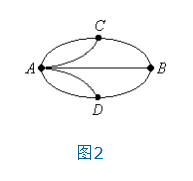
定义：

欧拉回路：图G=(V,E) (无向图or有向图) 的一个回路，如果恰通过图G的每一条边，则该回路称为欧拉回路，具有欧拉回路的图称为欧拉图。欧拉图就是从图上的一点出发，经过所有边且只能经过一次，最终回到起点的路径。

欧拉通路：即可以不回到起点，但是必须经过每一条边，且只能一次。也叫”一笔画”问题。

欧拉图与半欧拉图：具有欧拉回路的图称为欧拉图，具有欧拉通路而无欧拉回路的图称为半欧拉图。

桥：设无向图G=<V,E>，若存在边集E的一个非空子集E1，使得p(G-E1)>p(G)，而对于E1的任意真子集E2，均有p(G-E2)=p(G)，则称E1是G的边割集，或简称割集；若E1是单元集，即E1={e}，则称e为割边或桥。[p(G)表示图G的连通分支数.]

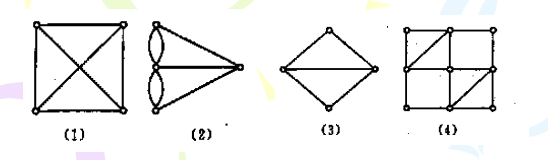
图中，图（4）为欧拉图，图（3）为半欧拉图，图（1）（2）不是欧拉图。

性质：

　　欧拉回路：一个欧拉回路，删掉一个点，仍然是一个欧拉回路。从一个欧拉回路拖走一个小欧拉回路，结果也是一个欧拉回路。

判定（充要）：

　　欧拉回路：1: 图G是连通的，不能有孤立点存在。

　　　　　　　2: 对于无向图来说度数为奇数的点个数为0;对于有向图来说每个点的入度必须等于出度。

　　欧拉通路：1: 图G是连通的，无孤立点存在。

　　　　　　　2: 对于无向图来说，度数为奇数的的点可以有2个或者0个，并且这两个奇点其中一个为起点另外一个为终点。对于有向图来说，可以存在两个点，其入度不等于出度，其中一个入度比出度大1，为路径的起点；另外一个出度比入度大1，为路径的终点。

算法（求欧拉回路）：

Fleury算法:

设图G是一个无向欧拉图，则按照下面算法求欧拉回路:

1:任取G中一个顶点v0,令P0 = v0.

2:假设沿Pi = v0e1v1e2v2……eivi 走到了顶点 vi,按照下面方法从E(i) = E(G) - {e1, e2, e3,…,ei} 中选e(i ＋　1),选择后删除e(i +１)这条边.

　　a):e(i+1)余vi关联

　　b):除非无别的边可选，否则e(i+1)不应是Gi = G – {e1,e2,…,ei} 中的桥.假若迫不得已选的是桥,除删除这条边之外,还应该再把孤立点从Gi中移除(选择桥边必然会形成孤立的点).

3:当步骤 2 无法继续执行时停止算法.

当算法停止时，所得到的简单回路 Pm = = v0e1v1e2v2e3v3……emvm (vm = v0) 为图G的一条欧拉回路.

下面用图来描述：

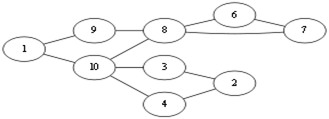
随便选择一个起点 v1。当前处在 v1 点，有两种走法 v1 – v9,v1 – v10，这俩条边都不是桥边，那么随便选择一个，<v1, v10>这条边吧。那么图就会成为这样.Eu = (走过的边集){<v1, v10>}

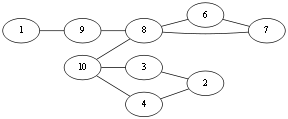
当前到了 V10 点，有<v10,v4>,<v10,v3>,<v10, v8>，先看<v10,v8>这条边吧，如果选择了这条边那么图就会成为这样：

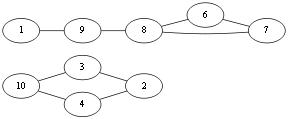
很显然形成了两个图，上下两个图不连通，即<v10, v8>这条边就是所谓的桥边，算法中说除非别无他选，否则不应该选择桥边，那么这条边就不能选择。回到上面，由于<v10,v4>,<v10,v3>都不是桥边，所以随便选择<v10,v4>吧. Eu={<v1, v10>,<v10,v4>}

到了 v4 这个点，<v4, v2>这条边是桥边,但是别无选择，只好选择这条边.选择完这条边这时不仅要从原图中删除这条边，由于点4成为了孤点，所以这个点也该从原图删除。Eu={<v1,v10>,<v10,v4>,<v4,v2>}.

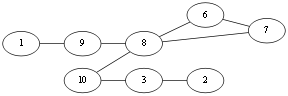
同理到达 v2 只好选择<v2,v3>，删除孤点 v2和边. Eu{<v1,v10>,<v10,v4>,<v4,v2><v2,v3>}.

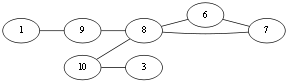
别无他选，<v3,v10>。Eu{<v1,v10>,<v10,v4>,<v4,v2><v2,v3><v3,v10>}.

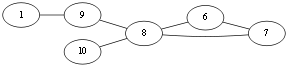
同样,选择<v10, v8>，Eu{<v1,v10>,<v10,v4>,<v4,v2><v2,v3><v3,v10>,<v10,v8>}.

此时到了 v8 同第一次到达v10时的情况，不能选择<v8,v9>这条桥边,选择<v8,v6>,Eu{<v1,v10>,<v10,v4>,<v4,v2><v2,v3><v3,v10>,<v10,v8>,<v8,v6>}.

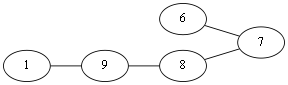
到达v6，选择<v6,v7>,删点删边,Eu{<v1,v10>,<v10,v4>,<v4,v2><v2,v3>,<v3,v10>,<v10,v8>,<v8,v6>,<v6,v7>}.以下就不给图了(逃;

然后接下来的选择都是别无他选,依次选择<v7,v8><v8,v9><v9,v1>，最后得到的欧拉边集Eu{<v1,v10>,<v10,v4>,<v4,v2><v2,v3>,<v3,v10>,<v10,v8>,<v8,v6>,<v6,v7>,<v7,v8><v8,v9><v9,v1>},于是我们就得到了一条欧拉回路.

算法实现：

这个算法在实现时也有很巧妙的方法。因为DFS本身就是一个入栈出栈的过程，所以我们直接利用DFS的性质来实现栈，其伪代码如下：

DFS(u):
	While (u存在未被删除的边e(u,v))
		删除边e(u,v)
		DFS(v)
	End
	PathSize ← PathSize + 1
	Path[ PathSize ] ← u

模板：

void DFS(Graph &G,SqStack &S,int x,int t)
{
       k=0;//一个标志,来标记当前访问的节点是否还有邻接边可供访问
       Push(S,x); //将本次遍历边所经由的点入栈
       for(i=t;i<v;i++) //v是顶点数,e是边数
        if(G[i][x]>0)  
         {
          k=1;
          G[i][x]=0; G[x][i]=0; //此边已访问,删除此边
          DFS(G,S,i,0);//寻找下一条关联的边,本次找到的是与x关联的i,在
                        //下一层中将寻找与i关联的边
          break;
         }//if,for
          if(k==0)       //如果k=0,说明与当前顶点关联的边已穷尽
       {
              Pop(S);
              GetTop(S,m);
              G[x][m]=1;G[m][x]=1;//恢复在上一层中被删除的边
              a=x+1;//如果可能的话,从当前节点的下一条关联边开始搜寻
              if(StackLength(S)!=e)//继续搜寻,边还没有全部遍历完
              {
                     Pop(S); //还原到上一步去
                     DFS(G,S,m,a);//
              }//if
              else   //搜寻完毕,将最后节点也入栈
                     Push(S,x);
       }//if
}//DFS
void Euler(Graph &G,int x)
{
//G是存储图的邻接矩阵,都处理成无向图形式,值为1代表有边,0代表无边,不包括自回路,x是出发点
InitStack(S);//用来存放遍历边时依次走过的顶点
DFS(G,S,x,0);//深度优先遍历查找,0是指查询的起点
//输出
 while(!StackEmpty(S))
 {
  GetTop(S,m);
  printf("->v%d",m);
  Pop(S);
 }//while
}//Euler

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string.h>
#include<algorithm>
#include<vector>
using namespace std;

const int N = 1005;
int n, m, flag, top, sum, du[N], ans[5005], map[N][N];

void dfs(int x)
{
    ans[++top] = x;
    for(int i = 1; i <= n; i++)
    {
        if(map[x][i] >= 1)
        {
            map[x][i]--;
            map[i][x]--;
            dfs(i);
            break;
        }
    }
}

void fleury(int x)
{
    top = 1;
    ans[top] = x;
    while(top > 0)
    {
        int k = 0;
        for(int i = 1; i <= n; i++)//判断是否可扩展
        {
            if(map[ans[top]][i] >= 1)//若存在一条从ans[top]出发的边  那么就是可扩展
            {k = 1; break;}
        }
        if(k == 0)//该点x没有其他的边可以先走了（即不可扩展）， 那么就输出它
        {
            printf("%d ", ans[top]);
            top--;
        }
        else if(k == 1)//如可扩展， 则dfs可扩展的哪条路线
        {
            top--;//这需要注意
            dfs(ans[top+1]);
        }
    }
}
int main()
{
    while(scanf("%d%d", &n, &m) != EOF)
    {
        memset(du, 0, sizeof(du));
        memset(map, 0, sizeof(map));

        for(int i = 1; i <= m; i++)
        {
            int x, y;
            scanf("%d%d", &x, &y);
            map[x][y]++; //记录边， 因为是无向图所以加两条边， 两个点之间可能有多条边
            map[y][x]++;
            du[x]++;
            du[y]++;
        }
        flag = 1; // flag标记开始点。 如果所有点度数全为偶数那就从1开始搜
        sum = 0;
        for(int i = 1; i <= n; i++)
        {
            if(du[i] % 2 == 1)
            {
                sum++;
                flag = i;// 若有奇数边， 从奇数边开始搜
            }
        }
        if(sum == 0 || sum == 2)
            fleury(flag);
    }
    return 0;
}

基本(套圈)法

1.在图中任意找一个回路C；

2.将图中属于C的边删除；

3.在残留图的各个极大连通分量中求欧拉回路；

4.将各极大连通分量中的欧拉回路合并到C上。

详细过程

　　首先从一个节点(v0)出发，随便往下走(走过的边需要标记一下，下次就别走了)，当走到不能再走的时候，所停止的点必然也是起点(因为所有的点的度数都是偶数，能进去肯定还会出来，再者中间有可能再次经过起点，但是如果起点还能继续走，那么就要继续往下搜索，直到再次回来时不能往下搜索为止)，然后停止时，走过的路径形成了一个圈，但因为是随便走的，所以可能有些边还没走就回来了，那些剩下的边肯定也会形成一个或者多个环，然后可以从刚才终止的节点往前回溯，找到第一个可以向其他方向搜索的节点(vi)，然后再以这个点继续往下搜索，同理还会继续回到该点(vi)，于是这个环加上上次那个环就构成了一个更大的环，即可以想象成形成了一条从 v0 到 vi的路径，再由 vi 走了一个环回到 vi，然后到达v0 的一条更长的路径，如果当前的路径还不是最长的，那么继续按照上面的方法扩展。只需要在回溯时记录下每次回溯的边，最后形成的边的序列就是一条欧拉回路。如果要记录点的顺序的话，那么每访问一个点，就把这个点压入栈中，当某个点不能继续搜索时，即在标记不能走的边是，这个点成为了某种意义上的孤点，然后把这个点输出最后得到的就是一条欧拉回路路径的点的轨迹。

　　总之，求欧拉回路的方法是，使用深度优先搜索，如果某条边被搜索到，则标记这条边为已选择，并且即使回溯也不能将当前边的状态改回未选择，每次回溯时，记录回溯路径。深度优先搜索结束后，记录的路径就是欧拉回路。

下面用图描述一遍：

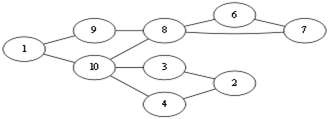
假设我们选择从v1开始走,由于随便走，所以可能出现以下走法

第一步：v1 – v9

第二步：v9 – v8

第三步：v8 – v10

第四步：v10 – v1

此时由于走过的边不能再走，那么从 v1 就无法继续向下探索,所以往前回溯,记录边集Eu{<v1, v10>}，此时回溯到 v10 ,发现可以继续走，那么

第五步: v10 – v3

第六步: v3 – v2

第七步: v2 – v4

第八步: v4 – v10

发现已经无路可走，那么继续回溯，记录回溯路径得到Eu{<v1,v10>, <v10, v4>, <v4, v2>, <v2, v3>, <v3, v10>, <v10, v8>}，此时回溯到了 v8.发现可以向其他方向搜索, 那么

第九步：v8 – v6

第十步：v6 –v7

第十一步：v7– v8

又无路可走，继续回溯Eu{<v1,v10>, <v10, v4>, <v4, v2>, <v2, v3>, <v3, v10>, <v10, v8>, <v8, v7>, <v7, v6>,<v6,v8>,<v8,v9>,<v9,v1>}，到这里整个DFS就结束了，我们得到的边集Eu就是一条欧拉回路。

具体实现与分析:

使用链式前向星和DFS实现寻找欧拉回路的算法，用链式前向星存无向边时每条边要存储两次。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <stack>
#include <queue>
using namespace std;

const int MAXV = 100 + 7;
const int MAXE = 100 * 100 + 7;
int head[MAXV];
int V, E;

typedef struct EdgeNode
{
    int to;
    int w;
    int next;   
}edgeNode;
edgeNode Edges[MAXE];

bool visit[2 * MAXE];
stack<int> stv;
queue<int> quv;//点集
queue<int> que;//边集

void EulerDFS(int now)
{
    st.push(now);//每访问一个点，就把该点压入栈
    for(int k = head[now]; k != -1; k = Edges[k].next)
    {
        if(!visit[k])
        {
            visit[k] = true;            //有向图每条边保存了两次，也要标记两次
            if(k & 1)
                visit[k + 1] = true;
            else
                visit[k - 1] = true;
            EulerDFS(Edges[k].to);
            que.push(k);//回溯时记录边
        }
    }
    quv.push(stv.top());//记录点
    stv.pop();
}

int main()
{
    //freopen("in.txt", "r", stdin);
    scanf("%d%d", &V, &E);
    memset(head, -1, sizeof(head));
    for(int i = 1; i <= E; i++)
    {
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        Edges[2 * i - 1].to = v;                //双向储存边
        Edges[2 * i - 1].w = w;
        Edges[2 * i - 1].next = head[u];
        head[u] = 2 * i - 1;
        Edges[2 * i].to = u;
        Edges[2 * i].w = w;
        Edges[2 * i].next = head[v];
        head[v] = 2 * i;
    }
    memset(visit, false, sizeof(visit));
    EulerDFS(1);
    return 0;
}

例题

例1

有N个盘子，每个盘子上写着一个仅由小写字母组成的英文单词。你需要给这些盘子按照合适的顺序排成一行，使得相邻两个盘子中，前一个盘子上面单词的末字母等于后一个盘子上面单词的首字母。请你编写一个程序，判断是否能达到这一要求。如果能，请给出一个合适的顺序。

分析

以26个英文字母作为顶点。对于每一个单词，在图中从它的首字母向末字母连一条有向边。

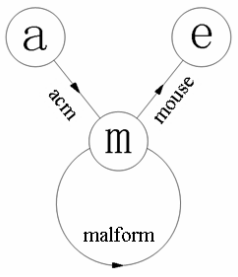
问题转化为在图中寻找一条不重复地经过所有边的路径，即欧拉路径。这个问题能够在O(|E|)时间内解决。

例2

PKU 2337

问题描述

给出一些字符串，让你首尾串起来串成一串，并且输出一个字典序最小的方案。如果不能，输出“**”。否则输出字典序最小的回路。

输入

aloha

arachnid

dog

gopher

rat

tiger

oak

maple

elm

输出

aloha.arachnid.dog.gopher.rat.tiger

分析

在没有特殊要求的情况下，DFS遍历图的结点顺序是可以任选的。但是这里由于加上了字典序最小的要求，所以DFS遍历时需要按照以下的优先顺序：

如果有不是桥的边，遍历这些边中字典序最小的边。

否则，遍历这些这些桥中字典序最小的边。

比如一个单词，abcde，那么就连接一条a到e的有向边。如此构成的图一共最多有26个节点。每条边都代表一个单词，那么就转化成了：找一条路，遍历所有的边。就是欧拉通路问题。

遍历欧拉通路的方法：

确定一个起点（出度-入度=1，或者等于0（如果存在欧拉回路的话））

从起点开始深搜（首先要保证图中存在欧拉回路或者通路）

dfs(vid, eid)

其中vid表示当前搜到的点。eid表示当前搜到的边（一个点可能会有很多边）

对于每条边，都是等它搜索完了后，把它代表的内容（这里是单词）压入一个栈中。

最后深搜结束后，依次弹栈就是答案。

例3

DOOR MAN

大意：给定N(<=20)个房间,房间之间有门相隔，门的数目不超过100道，当前人在第M个房门，当前人每经过一道门的时候就把经过的门锁上，问有没有一条路可以使得我们走到第0个房门的时候所有的门都锁上了。思路：我们可以把门看成是两个房间之间的边，那么问题可以转化成找一条欧拉路径。PS：判断的时候只要判断所有的边在一起就行了，所有的点不一定连通，当0点和M点不连通的时候，无解。注意这组数据。

中国邮递员问题(CPP)

定义

一个邮递员从邮局出发，要走完他所管辖范围内的每一条街道，至少一次再返回邮局，如何选择一条尽可能短的路线？这就是中国邮递员问题（CPP），其命名是因为中国数学家管梅谷在1962年首先提出了这个问题。如果用顶点表示交叉路口，用边表示街道，那么邮递员所管辖的范围可用一个赋权图来表示，其中边的权重表示对应街道的长度。

图论语言

中国邮递员问题可用图论语言叙述为：在一个具有非负权的赋权连通图G中，找出一条权最小的环游。这种环游称为最优环游。若G是欧拉图，则G的任意欧拉环游都是最优环游，从而可利用弗勒里算法求解。若G不是欧拉图，则G的任意一个环游必定通过某些边不止一次。将边e的两个端点再用一条权为w(e)的新边连接时，称边e为重复的。此时CPP与下述问题等价，若G是给定的有非赋权的赋权连通图，

（1）用添加重复边的方法求G的一个欧拉赋权母图，使得尽可能小；

（2）求的欧拉环游。

此图图论中和中国邮递员问题类似的是旅行商问题，区别于中国邮递员问题，旅行商问题是说在边赋权的完全图中找一个权和最小的哈密尔顿圈。

埃德蒙兹（J.Edmonds）和约翰逊（E.L.Johnson)在1973年给出了求解（1）的多项式时间算法。

如果邮递员所通过的街道都是单向道，则对应的图应为有向图。1973年，埃德蒙兹和约翰逊证明此时CPP也有多项式时间算法。帕帕季米特里屋（C.H.Papadimitrious）在1976年证明，如果既有双向道，又有单向道，则CPP是NP困难的。

分析

由于每边至少遍历一次，所以最短路的瓶颈就在于重复遍历。由于图一直保持连通性，所以两两奇点之间都存在欧拉路；又两两奇点之间的最短路可求；奇点个数为偶数。所以问题就等价于找一个奇点构成的完全图G’(V,E)的最小权匹配(Perfect Matching in General Graph)。V(G’)为原图G中的奇点，每条边为两奇点对应原图的最短路长度。

奇偶点图作业法

确定G中的奇点，构成G’。
确定G’两两结点在G中的最短路作为它们在G’中的边权。
对G’进行最小权匹配。
最小权匹配里的各匹配边所对应的路径在G中被重复遍历一次,得到欧拉图G’’。
对G’’找一条欧拉路即可。

有向的中国邮路问题，比较复杂。

哈密顿图（H问题）

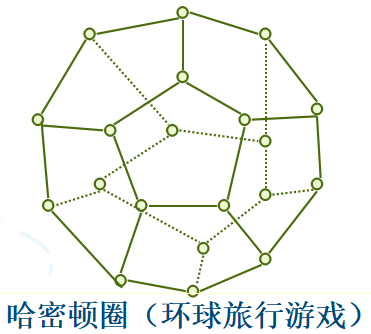
1857年，英国数学家汉密尔顿(Hamilton)提出了著名的汉密尔顿回路问题，其后，该问题进一步被发展成为所谓的“货郎担问题”，即赋权汉密尔顿回路最小化问题：这两个问题成为数学史上著名的难题。

性质

汉密尔顿路：给定图G，若存在一条路，经过图中每个结点恰好一次，这条路称作汉密尔顿路。

汉密尔顿回路：给定图G，若存在一条回路，经过图中每个结点恰好一次，这条回路称作汉密尔顿回路。

汉密尔顿图：具有汉密尔顿回路的图，称作汉密尔顿图。

解法

必须说明，汉密尔顿回路问题是一个NP完全问题(NP-Complete)，也就是说，至今没有一个行之有效的多项式时间的算法能够找到这类问题的最优解，只有一些近似算法。关于NPC问题，我们这里不做讨论。我们一般情况下，直接用DFS进行搜索，当然，如果图的点比较多的时候(一般n>10)，这个算法是不现实的。

旅行商问题(TSP)

Traveling Salesman Problem，即旅行商问题，旅行商人要拜访N个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值，这是一个NP难问题。

TSP的历史很久，最早的描述是1759年欧拉研究的骑士周游问题，即对于国际象棋棋盘中的64个方格，走访64个方格一次且仅一次，并且最终返回到起始点。

TSP由美国RAND公司于1948年引入，该公司的声誉以及线形规划]这一新方法的出现使得TSP成为一个知名且流行的问题。

解法

状压DP

着色问题

图的着色问题是由地图的着色问题引申而来的：用m种颜色为地图着色，使得地图上的每一个区域着一种颜色，且相邻区域颜色不同。问题处理：如果把每一个区域收缩为一个顶点，把相邻两个区域用一条边相连接，就可以把一个区域图抽象为一个平面图。

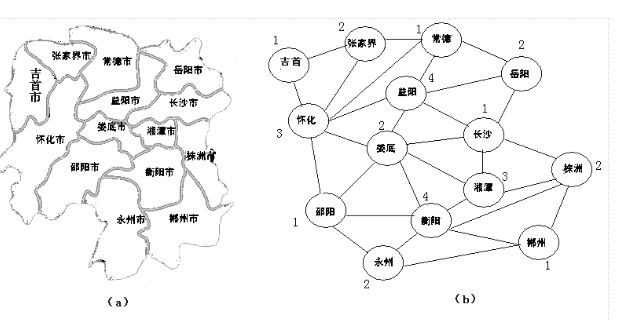
通常所说的着色问题是指下述两类问题：

1．给定无环图G=(V,E)，用m种颜色为图中的每条边着色，要求每条边着一种颜色，并使相邻两条边有着不同的颜色，这个问题称为图的边着色问题。

2．给定无向图G=(V,E)，用m种颜色为图中的每个顶点着色，要求每个顶点着一种颜色，并使相邻两顶点之间有着不同的颜色，这个问题称为图的顶着色问题。

边着色问题

定义：

给图G的边着色，使得有共同顶点的边异色的最少颜色数，称为边色数。

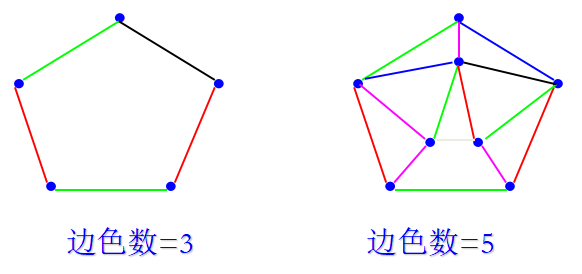
妖怪图（snark graph）

妖怪图每个点都关联着3条边，用4种颜色可以把每条边涂上颜色，使得有公共端点的边异色，而用3种颜色办不到，切断任意3条边不会使它断裂成2个有边的图。

单星妖怪和双星妖怪：

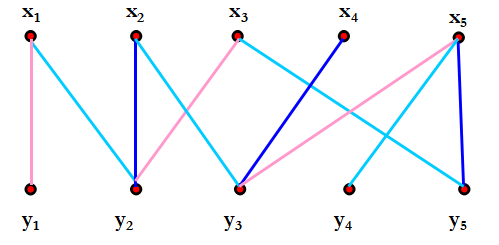
时间表问题；

设x1,x2,…,xm为m个工作人员，y1,y2,…,yn表为n种设备，工作人员对设备提出要求，使用时间均假定以单位时间计算，自然每一个工作人员在同一个时间只能使用一种设备，某一种设备在同一时间里只能为一个工作人员使用，问应如何合理安排，使得尽可能短时间里满足工作人员的要求？

问题转换为X={x1,x2,…,xm}，Y={y1,y2,…,yn}的二分图G，工作人员xi要求使用设备yj，每单位时间对应一条从xi到yj的边，这样所得的二分图过xi ，yj的边可能不止一条。问题变为对所得二分图G的边着色问题。有相同颜色的边可以安排在同一时间里。

定理：

二分图G的边色数＝图中顶点的最大度。

定理(Vizing 1964)：

若图G为简单图，图中顶点最大度为d，则G的边色数为d或d+1。

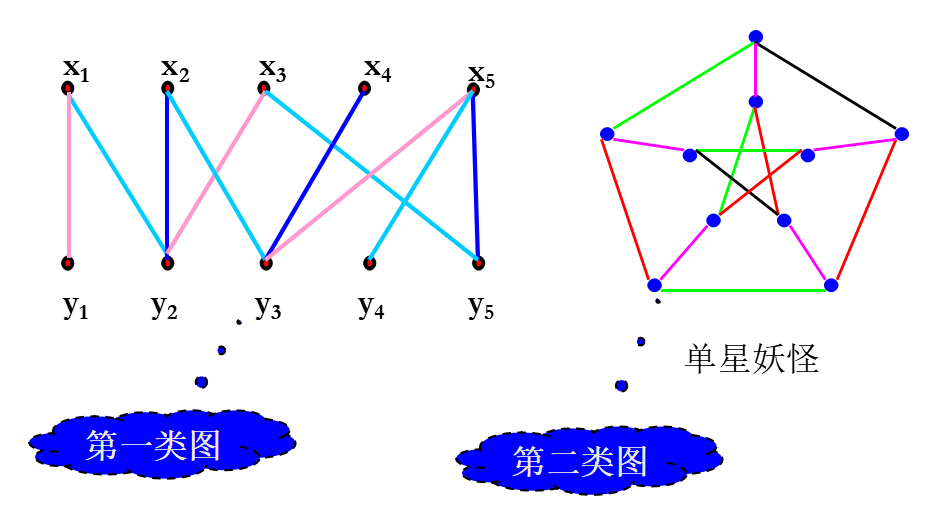
目前仍无有效区分(判别)任给定图属第几类图的有效方法。

引申

边的着色问题可以转化为顶点的着色问题。

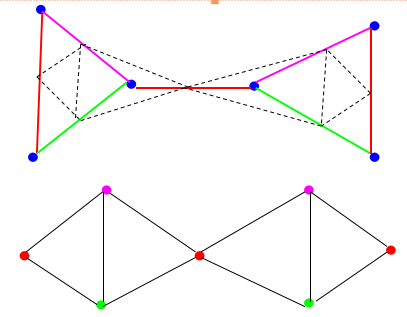
点着色问题

定义：

给图G的顶点着色，使得相邻的顶点异色的最少颜色数，称为图G顶色数，简称色数；记作χ(G)。

四色猜想：

平面图的色数不大于5。

色数的性质：

（1）图G只有孤立点时，χ(G)=1；

（2）n个顶点的完全图G有χ(G)=n；

（3）若图G是n个顶点的回路，则χ(G)=2， n为偶数。χ(G) =3， n为奇数；

（4）图G是顶点数超过1的树时，χ(G)=2；

（5）若图G是二分图，则χ(G)=2。

定理：

图G=(V,E)的色数χ(G)=2的充要条件是：(1)|E|≥1；(2)G不存在边数为奇数的回路。

若图G=(V,E)，d=max{d(vi)},vi∈V，则χ(G)≤d+1。