母函数
母函数是用于解决组合问题计数的一种方法。
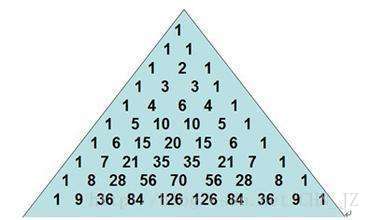
在了解它之前我们先看看熟悉的杨辉三角。
杨辉三角的第n行(注意是从0开始标号的)的数字就是(1+x)n(1+x)n的展开式从低项到高项的各项系数,也可以表示为组合数的形式CinCni。如果将两者联系起来我们会发现,(1+x)(1+x)可以看成对于一件取舍,1=x01=x0就是不取,x就是取。这样在(1+x)n(1+x)n的展开式中xixi项的系数就是从n件物品选取i件的方案数。
定义
给定数列a0,a1,a2…ana0,a1,a2…an,构造函数G(x)=a0f0(x)+a1f1(x)+a2f2(x)…anfn(x)G(x)=a0f0(x)+a1f1(x)+a2f2(x)…anfn(x),其中G(x)G(x)就是该序列的母函数,f0(x),f1(x),f2(x)…fn(x)f0(x),f1(x),f2(x)…fn(x)为标志函数。
母函数主要有两种形式:普通型母函数和指数型母函数。
普通型母函数
先看一个例题:HDU 1085
普通型母函数的标志函数一般为x0,x1,x2…xnx0,x1,x2…xn
因为每个硬币有个数限制,但是也不难构造出
G(x)=(1+x+x2+x3+…+xnum1)(1+x2+x4+…+x2∗num2)(1+x5+x10+…+x5∗num5)G(x)=(1+x+x2+x3+…+xnum1)(1+x2+x4+…+x2∗num2)(1+x5+x10+…+x5∗num5)
xixi
指数型母函数
再看一个例题:HDU 1521
指数型母函数的标志函数一般为x00!,x11!,x22!…xnn!x00!,x11!,x22!…xnn!,对于xii!xii!表示在一个方案中某个元素出现了ii次,而不同位置的该种元素本质不同,所以在记方案数时只算作一种,所以最后结果应处以i!i!。
对于这道题就不难构造出母函数为
G(x)=(1/ 0!+X / 1!+X2 / 2!+…+Xa1 / a1!)(1 / 0!+X / 1!+X2 / 2!+…+Xa2 / a2!)( / 0!+X / 1!+X2 / 2!+…+Xan / an!)