NAIPC2016-F.Mountain Scenes

1000ms
262144K

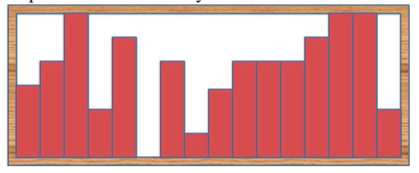
An artist begins with a roll of ribbon, one inch wide. She clips it into pieces of various integral lengths, then aligns them with the bottom of a frame, rising vertically in columns, to form a mountain scene. A mountain scene must be uneven; if all columns are the same height, it’s a plain scene, not a mountain scene! It is possible that she may not use all of the ribbon.

If our artist has 44 inches of ribbon and a 2 \times 22×2 inch frame, she could form these scenes:

She would not form these scenes, because they’re plains, not mountains!

Given the length of the ribbon and the width and height of the frame, all in inches, how many different mountain scenes can she create? Two scenes are different if the regions covered by ribbon are different. There’s no point in putting more than one piece of ribbon in any column.

Input

Each input will consist of a single test case. Note that your program may be run multiple times on different inputs. The input will consist of a single line with three space-separated integers nn, ww and hh, where nn (0 \le n \le 10,000)(0≤n≤10,000) is the length of the ribbon in inches, w (1 \le w \le 100)w(1≤w≤100) is the width and hh (1 \le h \le 100)(1≤h≤100)is the height of the frame, both in inches.

Output

Output a single integer, indicating the total number of mountain scenes our artist could possibly make, modulo 10^9 + 7109+7.

样例输入1复制

25 5 5

样例输出1复制

样例输入2复制

15 5 5

样例输出2复制

样例输入3复制

10 10 1

样例输出3复制

题解

问题可以转化为有n个物品，现有w个盘子，每个盘子的容量为[0,h]，所有盘子放的物品不能全部相同，n个物品选[0,n]个物品放进盘中，共有多少种方法。

首先，利用dp，第一层i为第i个盘子，第2层j为前i个盘子共放置j个物品共有多少种方法。这样dp[i][j]+=dp[i-1][j-k]，其中k[0,h]

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll maxn = 1e4+7;
const ll mod = 1e9+7;
ll dp[107][maxn];
ll n,w,h;
ll solve(){
    memset(dp,0,sizeof(dp));
    ll ans = 0;
    if(n > w * h){
        n = w*h;
    }
    for(int i = 0;i<=n;i++){
        dp[0][i] = 1;
    }
    for(int i = 1; i<=w; i++){
        for(int j = 0;j<=n; j++){
            for(int k = 0; k<=h&&k<=j; k++){
                dp[i][j]+=dp[i-1][j-k];
                dp[i][j]%=mod;
            }
        }
    }
    ans = (dp[w][n] - 1 - n/w + mod)%mod;
    return ans;
}
int main(){
    while(~scanf("%lld%lld%lld",&n,&w,&h)){
        printf("%lld\n",solve());
    }
    return 0;
}