剑指Offer题解及源码(C++完整版)

GitHub源码地址：https://github.com/qian-youyou/jzOffer

二维数组中的查找

题目描述

在一个二维数组中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

解析

首先选取数组中右上角的数字。如果该数字等于要查找的数字，查找过程结束；如果该数字大于要查找的数字，剔除这个数字所在的列；如果该数字小于要查找的数字，剔除这个数字所在的行。也就是说如果要查找的数字不在数组的右上角，则每一次都在数组的查找范围中剔除一行或者一列，这样每一步都可以缩小查找的范围，直到找到要查找的数字，或者查找范围为空。

　　例如，我们要在上述的二维数组中查找数字7的步骤如下图所示：

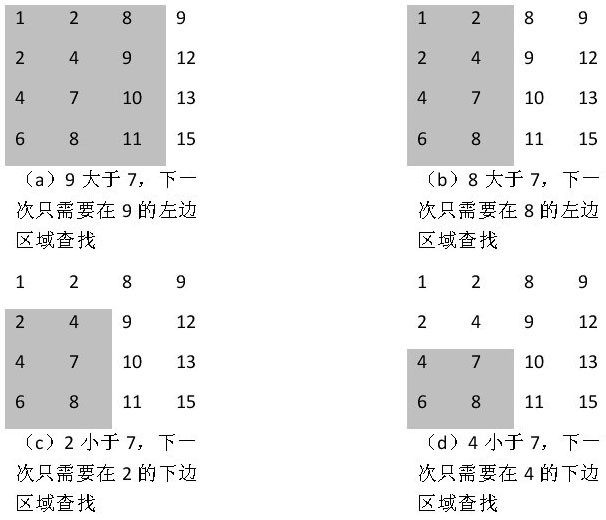
　　（矩阵中加阴影背景的区域是下一步查找的范围）

代码

class Solution {
public:
    bool Find(int target, vector<vector<int> > array) {
        int y = array.size();
        int x = array[0].size();
        int j = x - 1;
        int i = 0;
        while(j >=0 && i < y){
            if(array[i][j] == target){
                return true;
            }
            while(j >= 0 && array[i][j] > target){
                j--;
            }
            while(i < y && array[i][j] < target){
                i++;
            }
        }
        return false;
    }
};

替换空格

题目描述

请实现一个函数，将一个字符串中的每个空格替换成“%20”。例如，当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。

解析

将长度为1的空格替换为长度为3的“%20”，字符差的产度变长。如果允许我们开辟一个新的数组来存放替换空格后的字符串，那么这道题目就非常简 单。设置两个指针分别指向新旧字符串首元素，遍历原字符串，如果碰到空格就在新字符串上填入“%20”，否则就复制元字符串上的内容。但是如果面试官要求在原先的字符串上操作，并且保证原字符串有足够长的空间来存放替换后的字符串，那么我们就得另想方法。如果从前往后替换字符串，那么保存在空格后面的字符串肯定会被覆盖，那么我们就考虑从后往前进行替换。首先遍历原字符串，找出字符串的长度以及其中的空格数量，根据原字符串的长度和空格的数量我们可以求出最后新字符串的长度。设置两个指针point1和point2分别指向原字符串和新字符串的末尾位置。如果point1指向内容不为空格，那么将内容赋值给point2指向的位置，如果point1指向为空格，那么从point2开始赋值“02%”直到point1==point2时表明字符串中的所有空格都已经替换完毕。

代码

class Solution {
public:
	void replaceSpace(char *str,int length) {
        int cnt = 0;
        for(int i = 0; i < length; i++){
            if(str[i] == ' '){
                cnt++;
            }
        }
        int j = length + cnt * 2;
        for(int i = length; j>=0 && i >= 0; i--){
            if(str[i] != ' '){
                str[j--] = str[i];
            }
            else{
                str[j--] = '0';
                str[j--] = '2';
                str[j--] = '%';
            }
        }
	}
};

从尾到头打印链表

题目描述

输入一个链表，按链表值从尾到头的顺序返回一个ArrayList。

解析

遍历一遍链表，将每个结点value入栈。最后依次从栈中取出元素即可。

代码

/**
*  struct ListNode {
*        int val;
*        struct ListNode *next;
*        ListNode(int x) :
*              val(x), next(NULL) {
*        }
*  };
*/
class Solution {
public:
    vector<int> printListFromTailToHead(ListNode* head) {
        ListNode* p = head;
        stack<int>s;
        vector<int>v;
        while(p != NULL){
            s.push(p->val);
            p = p->next;
        }
        while(!s.empty()){
            v.push_back(s.top());
            s.pop();
        }
        return v;
    }
};

重建二叉树

题目描述

输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

解析

在二叉树的前序遍历序列中，第一个数字总是树的根结点的值。但在中序遍历序列中，根结点的值在序列的中间，左子树的结点的值位于根结点的值的左边，而右子树的结点的值位于根结点的值的右边。因此我们需要扫描中序遍历序列，才能找到根结点的值。

　　如下图所示，前序遍历序列的第一个数字1就是根结点的值。扫描中序遍历序列，就能确定根结点的值的位置。根据中序遍历特点，在根结点的值1前面的3个数字都是左子树结点的值，位于1后面的数字都是右子树结点的值。

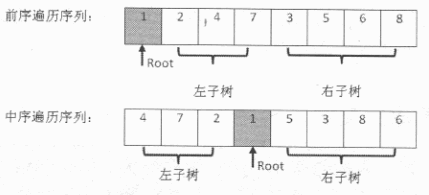
　　同样，在前序遍历的序列中，根结点后面的3个数字就是3个左子树结点的值，再后面的所有数字都是右子树结点的值。这样我们就在前序遍历和中序遍历两个序列中，分别找到了左右子树对应的子序列。

　　既然我们已经分别找到了左、右子树的前序遍历序列和中序遍历序列，我们可以用同样的方法分别去构建左右子树。也就是说，接下来的事情可以用递归的方法去完成。

代码

/**
 * Definition for binary tree
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin) {
        if(pre.size() == 0 || vin.size() == 0){
            return NULL;
        }
        TreeNode* T;
        int index = 0;
        buildTree(T, pre, vin, 0, 0, pre.size(), index);
        return T;
    }
    void buildTree(TreeNode* &T, vector<int> pre,vector<int> vin, int cur, int left, int right, int &index){
        T = new TreeNode(pre[cur]);
        ++index;
        int i;
        for(i = left; i < right; i++){
            if(vin[i] == pre[cur]){
                break;
            }
        }
        if(i > left && i < right){
            buildTree(T->left, pre, vin, cur + 1, left, i, index);
        }
        if(i < right - 1){
            buildTree(T->right, pre, vin, index, i + 1, right, index);
        }
    }
};

用两个栈实现队列

题目描述

用两个栈来实现一个队列，完成队列的Push和Pop操作。 队列中的元素为int类型。

解析

用stack1来实现队列的push操作，用stack2来实现队列的pop操作，当stack2为空时，将stack1的数据全部压入stack2，等待队列的pop操作。

代码

class Solution
{
public:
    void push(int node) {
        if(stack1.empty()){
            while(!stack2.empty()){
                stack1.push(stack2.top());
                stack2.pop();
            }
        }
        stack1.push(node);
    }

    int pop() {
        if(stack2.empty()){
            while(!stack1.empty()){
                stack2.push(stack1.top());
                stack1.pop();
            }
        }
        if(!stack2.empty()){
            int ans =  stack2.top();
            stack2.pop();
            return ans;
        }
        return 0;
    }

private:
    stack<int> stack1;
    stack<int> stack2;
};

旋转数组的最小数字

题目描述

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。 输入一个非减排序的数组的一个旋转，输出旋转数组的最小元素。 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。 NOTE：给出的所有元素都大于0，若数组大小为0，请返回0。

解析

由于数组非递减，那么旋转后的除了最小元素以外其他元素一定大于等于上一个元素，最小元素小于等于它上一个元素。遍历一遍查找哪个元素比上一元素小即可。若遍历完也没有，就输出第一个元素。

代码

class Solution {
public:
    int minNumberInRotateArray(vector<int> rotateArray) {
        int len = rotateArray.size();
        if(!len){
            return 0;
        }
        else if (len == 1){
            return rotateArray[0];
        }
        for(int i = 1; i < len; i++){
            if(rotateArray[i] < rotateArray[i - 1]){
                return rotateArray[i];
            }
        }
        return 0;
    }
};

斐波那契数列

题目描述

大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项（从0开始，第0项为0）。 n<=39

解析

斐波那契数列。F(N) = F(N - 1) + F(N - 2)

代码

class Solution {
public:
    int Fibonacci(int n) {
        int a[40];
        a[0] = 0;
        a[1] = 1;
        for(int i = 2; i < 40; i++){
            a[i] = a[i-1] + a[i-2];
        }
        return a[n];
    }
};

跳台阶

题目描述

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

解析

斐波那契数列。假设青蛙在第N阶，且第N-1阶跳法与第N-2阶跳法已经求出，则第N阶就是N-1阶的跳法加上第N-2阶的跳法。F(N) = F(N - 1) + F(N - 2)。

代码

class Solution {
public:
    int jumpFloor(int number) {
        if(number < 1){
            return 0;
        }
        vector<int>v(number + 1);
        v[0] = 1;
        v[1] = 1;
        for(int i = 2; i <= number; i++){
            v[i] = v[i-1] + v[i-2];
        }
        return v[number];
    }
};

变态跳台阶

题目描述

一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

解析

第N阶等于第1阶 + 第2阶 + …… + 第N-1阶。即2^(n-1)。

代码

class Solution {
public:
    int quick_pow(int n){
        int ans = 2, res = 1;
        while(n){
            if(n & 1){
                res *= ans;
            }
            ans *= ans;
            n >>= 1;
        }
        return res;
    }
    int jumpFloorII(int number) {
        number = quick_pow(number - 1);
        return number;
    }
};

矩形覆盖

题目描述

我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。请问用n个21的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

解析

骨牌最最简单的问题。依旧是斐波那契数列。

代码

class Solution {
public:
    int rectCover(int number) {
        if(number < 1){
            return 0;
        }
        vector<int>v(number + 1);
        v[0] = 1;
        v[1] = 1;
        for(int i = 2; i <= number; i++){
            v[i] = v[i-1] + v[i-2];
        }
        return v[number];
    }
};

二进制中1的个数

题目描述

输入一个整数，输出该数二进制表示中1的个数。其中负数用补码表示。

解析

位运算。时间复杂度为有几个1就执行几次。

代码

class Solution {
public:
     int  NumberOf1(int n) {
         int cnt = 0;
         while(n){
             cnt++;
             n = n & (n - 1);
         }
         return cnt;
     }
};

数值的整数次方

题目描述

给定一个double类型的浮点数base和int类型的整数exponent。求base的exponent次方。

解析

快速幂。

代码

class Solution {
public:
    double quick_pow(double base, int n){
        double ans = 1;
        while(n){
            if(n&1){
                ans *= base;
            }
            base*=base;
            n>>=1;
        }
        return ans;
    }
    double Power(double base, int exponent) {
        if(exponent >= 0){
            return quick_pow(base, exponent);
        }
        else{
            return pow(base, exponent);
        }
    }
};

调整数组顺序使奇数位于偶数前面

题目描述

输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有的奇数位于数组的前半部分，所有的偶数位于数组的后半部分，并保证奇数和奇数，偶数和偶数之间的相对位置不变。

解析

奇数储存于一个数组，偶数储存于一个数组。最后合并。

代码

class Solution {
public:
    void reOrderArray(vector<int> &array) {
        const int len = array.size();
        int a[len], b[len];
        int aa = 0;
        int bb = 0;
        for(int i = 0; i < len; i++){
            if(array[i]%2){
                a[aa++] = array[i];
            }
            else{
                b[bb++] = array[i];
            }
        }
        for(int i = 0; i < aa; i++){
            array[i] = a[i];
        }
        bb = 0;
        for(int i = aa; i < len; i++){
            array[i] = b[bb++];
        }
    }
};

链表中倒数第k个结点

题目描述

输入一个链表，输出该链表中倒数第k个结点。

解析

两个指针，一个指针先走k步，然后两个指针同时走，这样第1个指针走到头，第2给个指针刚好剩k个结点。

代码

/*
struct ListNode {
	int val;
	struct ListNode *next;
	ListNode(int x) :
			val(x), next(NULL) {
	}
};*/
class Solution {
public:
    ListNode* FindKthToTail(ListNode* pListHead, unsigned int k) {
        ListNode* p = pListHead;
        ListNode* q = pListHead;
        unsigned int cnt = 0;
        while(p != NULL){
            if(cnt >= k){
                q = q->next;
            }
            ++cnt;
            p = p->next;
        }
        if(cnt < k){
            return NULL;
        }
        return q;
    }
};

反转链表

题目描述

输入一个链表，反转链表后，输出新链表的表头。

解析

将前一个节点与后一个节点断开，然后让前一个节点指向后一个节点，这个过程就需要节点引用（可以理解为指针）来确定记录当前操作节点的前一个节点和后一个节点。

代码

/*
struct ListNode {
	int val;
	struct ListNode *next;
	ListNode(int x) :
			val(x), next(NULL) {
	}
};*/
class Solution {
public:
    ListNode* ReverseList(ListNode* pHead) {
        ListNode* p = NULL;
        ListNode* q = pHead;
        while(q){
            pHead = q;
            q = q->next;
            pHead->next = p;
            p = pHead;
        }
        return pHead;
    }
};

合并两个排序的链表

题目描述

输入两个单调递增的链表，输出两个链表合成后的链表，当然我们需要合成后的链表满足单调不减规则。

解析

归并排序基本操作。

代码

/*
struct ListNode {
	int val;
	struct ListNode *next;
	ListNode(int x) :
			val(x), next(NULL) {
	}
};*/
class Solution {
public:
    bool check(ListNode *a, ListNode *b){
        if(a == NULL || b == NULL){
            if(a != NULL){
                return true;
            }else{
                return false;
            }
        }
        return a->val < b->val;
    }
    void fun(ListNode* &p, ListNode* &pHead){
        ListNode* tmp = pHead;
        pHead = pHead->next;
        p->next = tmp;
        p = p->next;
    }
    ListNode* Merge(ListNode* pHead1, ListNode* pHead2)
    {
        ListNode* pHead = NULL;
        ListNode* p = pHead;
        while(pHead1 != NULL || pHead2 != NULL){
            if(check(pHead1, pHead2)){
                if(!pHead){
                    pHead = pHead1;
                    p = pHead;
                }
                else{
                    fun(p, pHead1);
                }
            }
            else{
                if(!pHead){
                    pHead = pHead2;
                    p = pHead;
                }
                else{
                    fun(p, pHead2);
                }
            }
        }
        return pHead;
    }
};

树的子结构

题目描述

输入两棵二叉树A，B，判断B是不是A的子结构。（ps：我们约定空树不是任意一个树的子结构）

解析

递归设计思路：

A、判断子树根值是否相等。

A1、如果是相等，需要一个可以判断该根左右孩子结点是否相等的递归函数。

A2、如果不等，找大树的左右孩子结点当根结点，递归到A步骤。

代码

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
    bool dfs(TreeNode* pRoot1, TreeNode* pRoot2){
        if(pRoot1 == NULL || pRoot2 == NULL){
            if(pRoot2 == NULL){
                return true;
            }else{
                return false;
            }
        }
        if(pRoot1->val == pRoot2->val){
            if(dfs(pRoot1->left, pRoot2->left)){
                if(dfs(pRoot1->right, pRoot2->right)){
                    return true;
                }
            }
        }
        return false;
    }
    bool HasSubtree(TreeNode* pRoot1, TreeNode* pRoot2)
    {
        if(pRoot1 == NULL || pRoot2 == NULL){
            return false;
        }
        if(pRoot1->val == pRoot2->val){
            if(dfs(pRoot1, pRoot2)){
                return true;
            }
        }
        bool flag = HasSubtree(pRoot1->left, pRoot2)||HasSubtree(pRoot1->right, pRoot2);
        return flag;
    }
};

二叉树的镜像

题目描述

操作给定的二叉树，将其变换为源二叉树的镜像。

输入描述:

二叉树的镜像定义：源二叉树 
    	    8
    	   /  \
    	  6   10
    	 / \  / \
    	5  7 9 11
    	镜像二叉树
    	    8
    	   /  \
    	  10   6
    	 / \  / \
    	11 9 7  5

解析

递归：

A：遍历左子树。

B：遍历右子树。

C：左子树和右子树交换。

代码

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
    void Mirror(TreeNode *pRoot) {
        if(pRoot == NULL){
            return;
        }
        if(pRoot->left != NULL){
            Mirror(pRoot->left);
        }
        if(pRoot->right != NULL){
            Mirror(pRoot->right);
        }
        TreeNode *tmp = pRoot->left;
        pRoot->left = pRoot->right;
        pRoot->right = tmp;
    }
};

顺时针打印矩阵

题目描述

输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字，例如，如果输入如下4 X 4矩阵： 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 则依次打印出数字1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10.

解析

用vis数组储存访问状态。每次直线走n-1个，如果vis已访问就改变方向。

代码

class Solution {
public:
    vector<int> printMatrix(vector<vector<int> > matrix) {
        vector<int>ans;
        const int len1 = matrix.size();
        if(!len1){
            return ans;
        }
        const int len2 = matrix[0].size();
        vector<bool>vis(len1*len2, false);
        int a[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
        bool flag = true;
        int x = 0, y = 0;
        ans.push_back(matrix[x][y]);
        vis[0] = true;
        while(flag){
            flag = false;
            for(int i = 0; i < 4; ++i){
                while(x + a[i][0] >= 0 && x + a[i][0] < len1 && y + a[i][1] >= 0 && y + a[i][1] < len2 && !vis[(x + a[i][0]) * len2 + y + a[i][1]]){
                    flag = true;
                    x += a[i][0];
                    y += a[i][1];
                    ans.push_back(matrix[x][y]);
                    vis[x*len2 + y] = true;
                }
            }
        }
        return ans;
    }
};

包含min函数的栈

题目描述

定义栈的数据结构，请在该类型中实现一个能够得到栈中所含最小元素的min函数（时间复杂度应为O（1））。

解析

两个栈，一个储存最小值，一个储存源数据。弹出的话两个一起弹出。

代码

class Solution {
public:
    void push(int value) {
        StackInt.push(value);
        if(StackMin.empty())
            StackMin.push(value);
        else if(StackMin.top()<value)
            StackMin.push(StackMin.top());
        else
            StackMin.push(value);
    }
    void pop() {
        if(!StackInt.empty())
        {
            StackInt.pop();
            StackMin.pop();
        }
    }
    int top() {
        return StackInt.top();
    }
    int min() {
        return StackMin.top();
    }
private:
    stack<int> StackInt;
    stack<int> StackMin;
};

栈的压入、弹出序列

题目描述

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。（注意：这两个序列的长度是相等的）

解析

栈模拟一遍即可。

代码

class Solution {
public:
    bool IsPopOrder(vector<int> pushV,vector<int> popV) {
        stack<int> s;
        int len = pushV.size(), i = 0, j = 0;
        while(i < len && j < len){
            while(s.empty() || i < len && s.top() != popV[j]){
                s.push(pushV[i++]);
            }
            while(j < len && !s.empty() && s.top() == popV[j]){
                s.pop();
                ++j;
            }
        }
        if(j < len){
            return false;
        }
        return true;
    }
};

从上往下打印二叉树

题目描述

从上往下打印出二叉树的每个节点，同层节点从左至右打印。

解析

广度优先遍历。queue储存数据。

代码

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
    vector<int> PrintFromTopToBottom(TreeNode* root) {
        vector<int>v;
        queue<TreeNode*>q;
        if(root == NULL){
            return v;
        }
        q.push(root);
        while(!q.empty()){
            TreeNode* tmp = q.front();
            q.pop();
            v.push_back(tmp->val);
            if(tmp->left != NULL){
                q.push(tmp->left);
            }
            if(tmp->right != NULL){
                q.push(tmp->right);
            }
        }
        return v;
    }
};

二叉搜索树的后序遍历序列

题目描述

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。

解析

对于一个二叉树的后序遍历序列来说，最后一个数一定是根节点，然后前面的数中，从最开始到第一个大于根节点的数都是左子树中的数，而后面到倒数第二个数应该都是大于根节点的，是右子树，如果后面的数中有小于根节点的，那么说明这个序列不是二叉搜索树的后序遍历序列。

代码

class Solution {
public:
    bool check(vector<int> &sequence, int left, int right){
        bool flag = false;
        if(left >= right){
            return true;
        }
        int mindle = left;
        int cur = sequence[right];
        for(int i = left; i < right; ++i){
            if(!flag && sequence[i] > cur){
                flag = true;
                mindle = i;
            }else if(flag && sequence[i] < cur){
                return false;
            }
        }
        flag = check(sequence, left, mindle - 1) && check(sequence, mindle, right - 1);
        return flag;
    }
    bool VerifySquenceOfBST(vector<int> sequence) {
        const int len = sequence.size();
        if(!len){
            return false;
        }
        return check(sequence, 0, len - 1);
    }
};

二叉树中和为某一值的路径

题目描述

输入一颗二叉树的跟节点和一个整数，打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。(注意: 在返回值的list中，数组长度大的数组靠前)

解析

首先思考节点值的和为输入的整数，每条路径都一定是从根节点到叶子节点，在数据结构中从根节点到叶子节点的遍历称之为深度优先遍历DFS。因此整个过程可以采用先序遍历方式的DFS，即根节点》左子树》右子树。随后考虑一次遍历完成后的处理，当一次遍历完成后，如果输入整数值恰好等于节点值之和，则输出这条路径并且回退一个节点；如果不等于则直接回退一个节点，即回退到当前节点的父节点，如果该父节点有右孩子，则继续遍历，否则继续回退。考虑回退到根节点，此时如果它有右孩子，则继续遍历，否则整个DFS结束。

代码

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
    vector<vector<int> > buffer;
    vector<int> tmp;
    vector<vector<int> > FindPath(TreeNode* root,int expectNumber) {
        if(root==NULL){
            return buffer;
        }
        tmp.push_back(root->val);
        if((expectNumber-root->val)==0 && root->left==NULL && root->right==NULL){
            buffer.push_back(tmp);
        }
        FindPath(root->left,expectNumber-root->val);
        FindPath(root->right,expectNumber-root->val);
        if(tmp.size()!=0){
            tmp.pop_back();
        }
        return buffer;
    }
};

复杂链表的复制

题目描述

输入一个复杂链表（每个节点中有节点值，以及两个指针，一个指向下一个节点，另一个特殊指针指向任意一个节点），返回结果为复制后复杂链表的head。（注意，输出结果中请不要返回参数中的节点引用，否则判题程序会直接返回空）

解析

第一步仍然是根据原始链表的每个结点N创建对应的N’。（把N’链接在N的后面）

第二步设置复制出来的结点的Sibling。（把N’的Sibling指向N的Sibling）

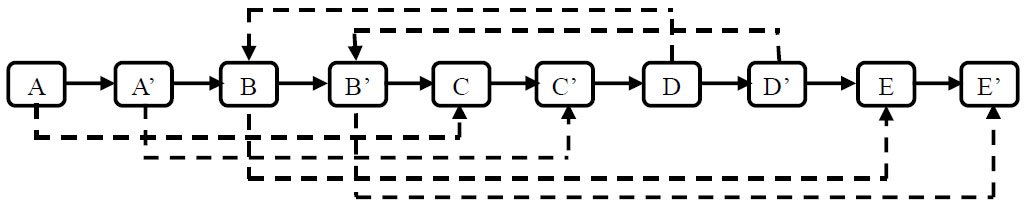
第三步把这个长链表拆分成两个链表：把奇数位置的结点用Next链接起来就是原始链表，偶数数值的则是复制链表。

代码

/*
struct RandomListNode {
    int label;
    struct RandomListNode *next, *random;
    RandomListNode(int x) :
            label(x), next(NULL), random(NULL) {
    }
};
*/
class Solution {
public:
    RandomListNode* Clone(RandomListNode* pHead)
    {
        RandomListNode *pHead2 = pHead, *p2, *tmp = pHead;
        while(tmp){
            p2 = new RandomListNode(tmp->label);
            p2->next = tmp->next;
            tmp->next = p2;
            tmp = p2->next;
        }
        if(pHead){
            pHead2 = pHead->next;
        }
        tmp = pHead;
        while(tmp){
            if(tmp->random){
                tmp->next->random = tmp->random->next;
            }
            tmp = tmp->next->next;
        }
        tmp = pHead;
        p2 = pHead2;
        while(tmp){
            tmp->next = tmp->next->next;
            tmp = tmp->next;
            if(p2->next){
                p2->next = p2->next->next;
                p2 = p2->next;
            }
        }
        return pHead2;
    }
};

二叉搜索树与双向链表

题目描述

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向。

解析

步骤1：递归左子树，使左子树为有序双向链表。

步骤2：递归右子树，使右子树为有序双向链表。

步骤3：左子树尾节点和根节点连接，右子树头节点和根节点连接。返回左子树头节点或根节点。

代码

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
    TreeNode* Convert(TreeNode* pRootOfTree){
        if(pRootOfTree){
            TreeNode* left = Convert(pRootOfTree->left);
            TreeNode* right = Convert(pRootOfTree->right);
            TreeNode* tail = left;
            if(right){
                right->left = pRootOfTree;
                pRootOfTree->right = right;
            }
            if(left){
                while(tail->right){
                    tail = tail->right;
                }
                tail->right = pRootOfTree;
                pRootOfTree->left = tail;
                return left;
            }
            return pRootOfTree;
        }
        return NULL;
    }
};

字符串的排列

题目描述

输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。

输入描述:

输入一个字符串,长度不超过9(可能有字符重复),字符只包括大小写字母。

解析

把一个字符串看成两部分组成：第一部分为第一个字符，第二部分为后面的所有字符。

求整个字符串的排列，可以看出两步：首先求所有可能出现在第一个位置的字符，即把第一个字符和后面的所有字符交换；然后固定第一个字符，求后面所有字符的排序。此时仍把后面的字符看成两部分，第一个字符和后面的字符，然后重复上述步骤。（递归）

在后面的在线测试中，要求输入字符串可能有重复的字符，输出按照字典顺序，排序即可。

代码

class Solution {
public:
    vector<string>v;
    void dfs(string str, int cur){
        if(cur < str.size() - 1){
            for(int i = cur; i < str.size(); ++i){
                if(i == cur || str[i] != str[cur]){
                    swap(str[cur], str[i]);
                    dfs(str, cur + 1);
                    swap(str[cur], str[i]);
                }
            }
        }else{
            v.push_back(str);
        }
    }
    vector<string> Permutation(string str) {
        dfs(str, 0);
        sort(v.begin(), v.end());
        return v;
    }
};

数组中出现次数超过一半的数字

题目描述

数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次，超过数组长度的一半，因此输出2。如果不存在则输出0。

解析

• 当我们遍历到下一个数字的时候，如果下一个数字和我们之前保存的数字相同，则次数加1；
• 如果下一个数字和我们之前保存的数字不同，则次数减1。
• 如果次数为零，我们需要保存下一个数字，并把次数设为1。
• 最后遍历一遍，统计该数出现的次数。

代码

class Solution {
public:
    int MoreThanHalfNum_Solution(vector<int> numbers) {
        const int len = numbers.size();
        if(!len){
            return 0;
        }
        int ans = numbers[0], cnt = 1;
        for(int i = 1; i < len; ++i){
            if(numbers[i] == ans){
                ++cnt;
            }else{
                if(!cnt){
                    ans = numbers[i];
                    cnt = 1;
                }
                --cnt;
            }
        }
        cnt = 0;
        for(int i = 0; i < len; ++i){
            if(numbers[i] == ans){
                ++cnt;
            }
        }
        if(cnt <= len / 2){
            ans = 0;
        }
        return ans;
    }
};

最小的K个数

题目描述

输入n个整数，找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字，则最小的4个数字是1,2,3,4,。

解析

建一个容量k的大根堆。

代码

class Solution {
public:
    vector<int> GetLeastNumbers_Solution(vector<int> input, int k) {
        vector<int>v;
        priority_queue<int>que;
        int len = input.size();
        if(len < k){
            return v;
        }
        for(int i = 0; i < len; ++i){
            que.push(input[i]);
            while(que.size() > k){
                que.pop();
            }
        }
        while(!que.empty()){
            v.push_back(que.top());
            que.pop();
        }
        return v;
    }
};

连续子数组的最大和

题目描述

HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。今天测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢？例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。给一个数组，返回它的最大连续子序列的和，你会不会被他忽悠住？(子向量的长度至少是1)

解析

直接遍历，如果上一个数加上这个数变小了就不加，否则加上。

代码

class Solution {
public:
    int FindGreatestSumOfSubArray(vector<int> array) {
        int len = array.size();
        int ans = array[0];
        for(int i = 1; i < len; ++i){
            array[i] = max(array[i], array[i] + array[i - 1]);
            ans = max(ans, array[i]);
        }
        return ans;
    }
};

整数中1出现的次数（从1到n整数中1出现的次数）

题目描述

求出1~13的整数中1出现的次数,并算出100~1300的整数中1出现的次数？为此他特别数了一下1~13中包含1的数字有1、10、11、12、13因此共出现6次,但是对于后面问题他就没辙了。ACMer希望你们帮帮他,并把问题更加普遍化,可以很快的求出任意非负整数区间中1出现的次数（从1 到 n 中1出现的次数）。

解析

总结一下以上的算法，可以看到，当计算右数第 i 位包含的 x 的个数时：

• 取第 i位左边(高位)的数字，乘以 10i-1，得到基础值 a
• 取第 i 位数字，计算修正值
• 如果大于 x , 则结果为 a + 10i-1
• 如果小于 x，则结果为 a
• 如果等于 x，则取第 i 位右边(低位)数字，设为 b，最后结果为 a + b + 1

代码

class Solution {
public:
    int NumberOf1Between1AndN_Solution(int n)
    {
        int cnt = n, ans = 0, res = 1;
        while(cnt){
            if(cnt % 10){
                if(cnt % 10 > 1){
                    ans += res;
                }else{
                    ans += n % res + 1;
                }
                
            }
            cnt /= 10;
            ans += cnt * res;
            res *= 10;
        }
        return ans;
    }
};

把数组排成最小的数

题目描述

输入一个正整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。例如输入数组{3，32，321}，则打印出这三个数字能排成的最小数字为321323。

解析

sort排序即可，cmp由我们写，可以转成字符串，然后利用字符串进行比较。

代码

class Solution {
public:
    static bool cmp(int a, int b){
        string str1 = to_string(a);
        string str2 = to_string(b);
        return str1 + str2 < str2 + str1;
    }
    string PrintMinNumber(vector<int> numbers) {
        int tmp;
        string str;
        int len = numbers.size();
        sort(numbers.begin(), numbers.end(), cmp);
        for(int i = 0; i < len; ++i){
            while(numbers[i] == 0){
                continue;
            }
            str += to_string(numbers[i]);
        }
        return str;
    }
};

丑数

题目描述

把只包含质因子2、3和5的数称作丑数（Ugly Number）。例如6、8都是丑数，但14不是，因为它包含质因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。

解析

优先队列+集合+选择性插入

代码

class Solution {
public:
    int GetUglyNumber_Solution(int index) {
        priority_queue<int, vector<int>, greater<int> >que;
        que.push(1);
        int i = 0;
        int MAXN = 0;
        set<int>s;
        while(!que.empty()){
            int ans = que.top();
            que.pop();
            if(s.count(ans)||ans < 0){
                continue;
            }
            s.insert(ans);
            ++i;
            s.insert(ans);
            if(i == index){
                return ans;
            }
            if(que.size() < index){
                que.push(ans*2);
                que.push(ans*3);
                que.push(ans*5);
                MAXN = max(MAXN, ans * 5);
            }
            else{
                if(ans*2<MAXN){
                    que.push(ans*2);
                }
                if(ans*3<MAXN){
                    que.push(ans*3);
                }
                if(ans*5<MAXN){
                    que.push(ans*5);
                }
            }
        }
        return 0;
    }
};

第一个只出现一次的字符

题目描述

在一个字符串(0<=字符串长度<=10000，全部由字母组成)中找到第一个只出现一次的字符,并返回它的位置, 如果没有则返回 -1（需要区分大小写）.

解析

哈希表，可用map统计。

代码

class Solution {
public:
    int FirstNotRepeatingChar(string str) {
        map<char, int>m;
        for(int i = 0; i < str.length(); i++){
            m[str[i]]++;
        }
        for(int i = 0; i < str.length(); i++){
            if(m[str[i]] == 1){
                return i;
            }
        }
        return -1;
    }
};

数组中的逆序对

题目描述

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007

输入描述:

题目保证输入的数组中没有的相同的数字数据范围：	对于%50的数据,size<=10^4	对于%75的数据,size<=10^5	对于%100的数据,size<=2*10^5

示例1

输入

1,2,3,4,5,6,7,0

输出

7

解析

归并排序。先把数组分割成子数组，先统计出子数组内部的逆序对的数目，然后再统计出两个相邻子数组之间的逆序对的数目。在统计逆序对的过程中，还需要对数组进行排序。如果对排序算法很熟悉，我们不难发现这个过程实际上就是归并排序。

代码

class Solution {
public:
    const long long mod = 1e9 + 7;
    int my_merge(vector<int> &data, int left, int mindle, int right){
        vector<int>A(mindle - left + 1);
        vector<int>B(right - mindle);
        long long ans = 0;
        for(int i = left; i <= mindle; ++i){
            A[i - left] = data[i];
        }
        for(int i = mindle + 1; i <= right; ++i){
            B[i - mindle - 1] = data[i];
        }
        int x = 0, y = 0;
        for(int i = left; i <= right; ++i){
            if(x >= A.size()){
                data[i] = B[y++];
            }else if(y >= B.size()){
                data[i] = A[x++];
            }else{
                if(A[x] > B[y]){
                    data[i] = B[y++];
                    ans += A.size() - x;
                }else{
                    data[i] = A[x++];
                }
            }
        }
        ans %= mod;
        return ans;
    }
    int mergeSort(vector<int>&data, int left, int right){
        long long ans = 0;
        if(left < right){
            int mindle = (left + right) / 2;
            ans += mergeSort(data, left, mindle);
            ans += mergeSort(data, mindle + 1, right);
            ans += my_merge(data, left, mindle, right);
        }
        ans %= mod;
        return ans;
    }
    int InversePairs(vector<int> data) {
        int ans = mergeSort(data, 0, data.size() - 1);
        return ans;
    }
};

两个链表的第一个公共结点

题目描述

输入两个链表，找出它们的第一个公共结点。

解析

如果两链表有交点，则必然是“Y”型或“V”型。

如何判断两个单向链表有没有公共结点？如果两个链表有一个公共结点，那么 该公共结点之后的所有结点都是重合的。那么，它们的最后一个结点必然是重合的。因此，我们判断两个链表是不是有重合的部分，只要分别遍历两个链表到最后一 个结点。如果两个尾结点是一样的，说明它们用重合；否则两个链表没有公共的结点。

在上面的思路中，顺序遍历两个链表到尾结点的时候，我们不能保证在两个链表上同时到达尾结点。这是因为两个链表不一定长度一样。但如果假设一个链表比另一个长l个结点，我们先在长的链表上遍历l个结点，之后再同步遍历，这个时候我们就能保证同时到达最后一个结点了。由于两个链表从第一个公共结点考试到链表的尾结点，这一部分是重合的。因此，它们肯定也是同时到达第一公共结点的。于是在遍历中，第一个相同的结点就是第一个公共的结点。

在这个思路中，我们先要分别遍历两个链表得到它们的长度，并求出两个长度之差。在长的链表上先遍历若干次之后，再同步遍历两个链表，知道找到相同的结点，或者一直到链表结束。此时，如果第一个链表的长度为m，第二个链表的长度为n，该方法的时间复杂度为O(m+n)。

代码

/*
struct ListNode {
	int val;
	struct ListNode *next;
	ListNode(int x) :
			val(x), next(NULL) {
	}
};*/
class Solution {
public:
    ListNode* fun(ListNode* &pHead, ListNode* p){
        ListNode* q = pHead;
        while(p != NULL){
            p = p->next;
            q = q->next;
        }
        return q;
    }
    ListNode* FindFirstCommonNode( ListNode* pHead1, ListNode* pHead2) {
        ListNode* p1 = pHead1;
        ListNode* p2 = pHead2;
        while(p1 != NULL && p2 != NULL){
            if(p1 == p2){
                return p1;
            }
            p1 = p1->next;
            p2 = p2->next;
        }
        if(p1 == NULL && p2 == NULL){
            return NULL;
        }else{
            if(p1 != NULL){
                p1 = fun(pHead1, p1);
                p2 = pHead2;
            }else{
                p2 = fun(pHead2, p2);
                p1 = pHead1;
            }
        }
        return FindFirstCommonNode(p1, p2);
    }
};

数字在排序数组中出现的次数

题目描述

统计一个数字在排序数组中出现的次数。

解析

我的方法直接遍历。更高效的方法是二分查找两遍，先找到该数字的左边界，再找到该数字的右边界，然后下标相减。

代码

class Solution {
public:
    int GetNumberOfK(vector<int> data ,int k) {
        int cnt = 0;
        for(int i = 0; i < data.size(); ++i){
            if(data[i] == k){
                ++cnt;
            }
        }
        return cnt;
    }
};

二叉树的深度

题目描述

输入一棵二叉树，求该树的深度。从根结点到叶结点依次经过的结点（含根、叶结点）形成树的一条路径，最长路径的长度为树的深度。

解析

遍历一遍即可。

代码

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
    int TreeDepth(TreeNode* pRoot)
    {
        int cnt = 0;
        if(pRoot != NULL){
            cnt += max(TreeDepth(pRoot->left), TreeDepth(pRoot->right)) + 1;
        }
        return cnt;
    }
};

平衡二叉树

题目描述

输入一棵二叉树，判断该二叉树是否是平衡二叉树。

解析

递归判断左子树深度和右子树深度差是否不大于1。

代码

class Solution {
public:
    bool IsBalanced_Solution(TreeNode* pRoot) {
        if(pRoot == NULL)
            return true;
        int leftDepth = getDepth(pRoot -> left);
        int rightDepth = getDepth(pRoot -> right);
        if(leftDepth > rightDepth + 1 || leftDepth + 1 < rightDepth)
            return false;
        else
            return IsBalanced_Solution(pRoot -> left) && IsBalanced_Solution(pRoot -> right);
    }
     
    int getDepth(TreeNode* pRoot){
        if(pRoot == NULL)
            return 0;
        int leftDepth = getDepth(pRoot -> left);
        int rightDepth = getDepth(pRoot -> right);
        return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
    }
};

数组中只出现一次的数字

题目描述

一个整型数组里除了两个数字之外，其他的数字都出现了两次。请写程序找出这两个只出现一次的数字。

解析

我用的map。可以用位运算。

代码

class Solution {
public:
    void FindNumsAppearOnce(vector<int> data,int* num1,int *num2) {
        int len = data.size();
        bool flag = false;
        map<int, int>m;
        for(int i = 0; i < len; ++i){
            m[data[i]]++;
        }
        for(int i = 0; i < len; ++i){
            if(m[data[i]] == 1){
                if(flag){
                    *num2 = data[i];
                }else{
                    flag = true;
                    *num1 = data[i];
                }            
            }
        }
    }
};

和为S的连续正数序列

题目描述

小明很喜欢数学,有一天他在做数学作业时,要求计算出9~16的和,他马上就写出了正确答案是100。但是他并不满足于此,他在想究竟有多少种连续的正数序列的和为100(至少包括两个数)。没多久,他就得到另一组连续正数和为100的序列:18,19,20,21,22。现在把问题交给你,你能不能也很快的找出所有和为S的连续正数序列? Good Luck!

输出描述:

输出所有和为S的连续正数序列。序列内按照从小至大的顺序，序列间按照开始数字从小到大的顺序

解析

在序列首部各定义指针left, right，如果和超过s，left往右移，如果和小于s，right往右移。

代码

class Solution {
public:
    vector<vector<int> > FindContinuousSequence(int sum) {
        vector<int> v;
        vector<vector<int> >ans;
        for(int i = 1; i <= sum; ++i){
            v.push_back(i);
        }
        int left = 1, right = 1;
        int cnt = 1;
        while(right < sum && left < sum){
            if(cnt == sum){
                ans.push_back(vector<int>(v.begin() + left - 1, v.begin() + right));
            }
            if(cnt > sum){
                cnt -= left;
                ++left;
            }else if(cnt <= sum){
                ++right;
                cnt += right;
            }
        }
        return ans;
    }
};

和为S的两个数字

题目描述

输入一个递增排序的数组和一个数字S，在数组中查找两个数，使得他们的和正好是S，如果有多对数字的和等于S，输出两个数的乘积最小的。

输出描述:

对应每个测试案例，输出两个数，小的先输出。

解析

在序列首尾各定义指针p1, p2，如果和超过s，p2往中间移，如果和小于s，p1往中间移。

代码

class Solution {
public:
    vector<int> FindNumbersWithSum(vector<int> array,int sum) {
        vector<int>v;
        int left = 0;
        int right = array.size() - 1;
        while(left < right){
            if(array[left] + array[right] == sum){
                v.push_back(array[left]);
                v.push_back(array[right]);
                break;
            }else if(array[left] + array[right] > sum){
                --right;
            }else{
                ++left;
            }
        }
        return v;
    }
};

左旋转字符串

题目描述

汇编语言中有一种移位指令叫做循环左移（ROL），现在有个简单的任务，就是用字符串模拟这个指令的运算结果。对于一个给定的字符序列S，请你把其循环左移K位后的序列输出。例如，字符序列S=”abcXYZdef”,要求输出循环左移3位后的结果，即“XYZdefabc”。是不是很简单？OK，搞定它！

解析

先取余，再字符串分割。

代码

class Solution {
public:
    string LeftRotateString(string str, int n) {
        unsigned int len = str.size();
        if(!len){
            return "";
        }
        n %= len;
        string str2 = str.substr(size_t(n)) + str.substr(0, n);
        return str2;
    }
};

翻转单词顺序列

题目描述

牛客最近来了一个新员工Fish，每天早晨总是会拿着一本英文杂志，写些句子在本子上。同事Cat对Fish写的内容颇感兴趣，有一天他向Fish借来翻看，但却读不懂它的意思。例如，“student. a am I”。后来才意识到，这家伙原来把句子单词的顺序翻转了，正确的句子应该是“I am a student.”。Cat对一一的翻转这些单词顺序可不在行，你能帮助他么？

解析

用栈储存单词，存完了再输出。

代码

class Solution {
public:
    string ReverseSentence(string str) {
        stack<string>s;
        istringstream istring;
        istring.str(str);
        string tmp;
        while(istring >> tmp){
            s.push(tmp);
        }
        if(!s.empty()){
            s.pop();
        }else{
            if(str.size()){
                return str;
            }
        }
        while(!s.empty()){
            tmp += " " + s.top();
            s.pop();
        }
        return tmp;
    }
};

扑克牌顺子

题目描述

LL今天心情特别好,因为他去买了一副扑克牌,发现里面居然有2个大王,2个小王(一副牌原本是54张^_^)…他随机从中抽出了5张牌,想测测自己的手气,看看能不能抽到顺子,如果抽到的话,他决定去买体育彩票,嘿嘿！！“红心A,黑桃3,小王,大王,方片5”,“Oh My God!”不是顺子…..LL不高兴了,他想了想,决定大\小 王可以看成任何数字,并且A看作1,J为11,Q为12,K为13。上面的5张牌就可以变成“1,2,3,4,5”(大小王分别看作2和4),“So Lucky!”。LL决定去买体育彩票啦。 现在,要求你使用这幅牌模拟上面的过程,然后告诉我们LL的运气如何， 如果牌能组成顺子就输出true，否则就输出false。为了方便起见,你可以认为大小王是0。

解析

暴力做的。

代码

class Solution {
public:
    bool IsContinuous( vector<int> numbers ) {
        if(numbers.empty()){
            return false;
        }
        int cnt = 0, cur = 0;
        sort(numbers.begin(), numbers.end());
        for(int i = 0; i < numbers.size(); ++i){
            if(numbers[i] == 0){
                ++cnt;
            }else{
                if(cur){
                    while(numbers[i] != cur + 1){
                        cur += 1;
                        --cnt;
                        if(cnt < 0){
                            return false;
                        }
                    }
                    cur += 1;
                }
                else{
                    cur = numbers[i];
                }
            }
        }
        return true;
    }
};

孩子们的游戏(圆圈中最后剩下的数)

题目描述

每年六一儿童节,牛客都会准备一些小礼物去看望孤儿院的小朋友,今年亦是如此。HF作为牛客的资深元老,自然也准备了一些小游戏。其中,有个游戏是这样的:首先,让小朋友们围成一个大圈。然后,他随机指定一个数m,让编号为0的小朋友开始报数。每次喊到m-1的那个小朋友要出列唱首歌,然后可以在礼品箱中任意的挑选礼物,并且不再回到圈中,从他的下一个小朋友开始,继续0…m-1报数….这样下去….直到剩下最后一个小朋友,可以不用表演,并且拿到牛客名贵的“名侦探柯南”典藏版(名额有限哦!!^_^)。请你试着想下,哪个小朋友会得到这份礼品呢？(注：小朋友的编号是从0到n-1)

解析

现在我们把他们的编号做一下转换：

k –> 0
k+1 –> 1
k+2 –> 2
…
…
k-2 –> n-2
k-1 –> n-1
解x’ —-> 解为x
注意< x’就是最终的解 >

变换后就完完全全成为了(n-1)个人报数的子问题，假如我们知道这个子问题的解：例如x是最终的胜利者，那么根据上面这个表把这个x变回去不刚好就是n个人情况的解吗？！！变回去的公式很简单，相信大家都可以推出来：x’=(x+k)%n

如何知道(n-1)个人报数的问题的解？对，只要知道(n-2)个人的解就行了。(n-2)个人的解呢？当然是先求(n-3)的情况 —- 这显然就是一个倒推问题！下面举例说明：

假设现在是6个人（编号从0到5）报数，报到（2-1）的退出，即 < m=2>。那么第一次编号为1的人退出圈子，从他之后的人开始算起，序列变为2,3,4,5,0，即问题变成了这5个人报数的问题，将序号做一下转换：
2 –>0
3 –>1
4 –>2
5 –>3
0 –>4
现在假设x为0,1,2,3,4的解，x’设为那么原问题的解（这里注意，2,3,4,5,0的解就是0,1,2,3,4,5的解，因为1出去了，结果还是一个），根据观察发现，x与x’关系为x’=(x+m)%n，因此只要求出x，就可以求x’。x怎么求出呢？继续推导吧。0,1,2,3,4,，同样是第二个1出列，变为（2,3,4,0），转换下为
2 –>0
3 –>1
4 –>2
0 –>3
很简单，同样的道理，公式又出来了，x=(x”+m)%5，这里变成5了。即求n-1个人的问题就是找出n-2的人的解，n-2就是要找出n-3，等等
因此，就可以回去看上面的推导过程了。

好了，思路出来了，下面写递推公式：
令f[i]表示i个人玩游戏报m退出最后胜利者的编号，最后的结果自然是f[n]

递推公式
f[1]=0;
f[i]=(f[i-1]+m)%i; (i>1)

有了这个公式，我们要做的就是从1-n顺序算出f[i]的数值，最后结果是f[n]。因为实际生活中编号总是从1开始，我们输出f[n]+1
由于是逐级递推，不需要保存每个f[i]。

代码

class Solution {
public:
    int LastRemaining_Solution(int n, int m)
    {
        if(n + m == 0){
            return -1;
        }
        int s = 0;
        for(int i = 2; i <= n; ++i){
            s = (s + m) % i;
        }
        return s;
    }
};

求1+2+3+…+n

题目描述

求1+2+3+…+n，要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句（A?B:C）。

解析

利用逻辑运算符&&的性质。

代码

class Solution {
public:
    int Sum_Solution(int n) {
        return fun(n);
    }
    int fun(int n){
        n && (n += fun(n-1));
        return n;
    }
};

不用加减乘除做加法

题目描述

写一个函数，求两个整数之和，要求在函数体内不得使用+、-、*、/四则运算符号。

解析

位运算，先异或，再右移。

代码

class Solution {
public:
    int Add(int num1, int num2)
    {
        while(num2){
            int a1 = num1 ^ num2;
            int a2 = num1 & num2;
            a2 <<= 1;
            num1 = a1;
            num2 = a2;
        }
        return num1;
    }
};

把字符串转换成整数

题目描述

将一个字符串转换成一个整数(实现Integer.valueOf(string)的功能，但是string不符合数字要求时返回0)，要求不能使用字符串转换整数的库函数。 数值为0或者字符串不是一个合法的数值则返回0。

输入描述:

输入一个字符串,包括数字字母符号,可以为空

输出描述:

如果是合法的数值表达则返回该数字，否则返回0

示例1

输入

+2147483647
    1a33

输出

2147483647
    0

解析

暴力

代码

class Solution {
public:
    int StrToInt(string str) {
        int ans = 0;
        int flag = 0;
        for(int i = 0; i < str.length(); i++){
            while(str[i] == ' '){
                continue;
            }
            if(str[i] <= '9' && str[i] >= '0'){
                ans *= 10;
                ans += str[i] - '0';
            }else{
                if(!flag){
                    if(str[i] == '-'){
                        flag = -1;
                    }else if(str[i] == '+'){
                        flag = 1;
                    }else{
                        return 0;
                    }
                }else{
                    return 0;
                }
            }
        }
        if(flag){
            ans *= flag;
        }
        return ans;
    }
};

数组中重复的数字

题目描述

在一个长度为n的数组里的所有数字都在0到n-1的范围内。 数组中某些数字是重复的，但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。 例如，如果输入长度为7的数组{2,3,1,0,2,5,3}，那么对应的输出是第一个重复的数字2。

解析

0~n-1正常的排序应该是A[i]=i；因此可以通过交换的方式，将它们都各自放回属于自己的位置；

从头到尾扫描数组A，当扫描到下标为i的数字m时，首先比较这个数字m是不是等于i，

如果是，则继续扫描下一个数字；

如果不是，则判断它和A[m]是否相等，如果是，则找到了第一个重复的数字（在下标为i和m的位置都出现了m）；如果不是，则把A[i]和A[m]交换，即把m放回属于它的位置；

重复上述过程，直至找到一个重复的数字；

时间复杂度：O(n)，空间复杂度：O(1)

注：张氏排序法

代码

class Solution {
public:
    // Parameters:
    //        numbers:     an array of integers
    //        length:      the length of array numbers
    //        duplication: (Output) the duplicated number in the array number
    // Return value:       true if the input is valid, and there are some duplications in the array number
    //                     otherwise false
    bool duplicate(int numbers[], int length, int* duplication) {
        for(int i = 0; i < length; ++i){
            while(numbers[i] != i){
                if(numbers[i] == numbers[numbers[i]]){
                    *duplication = numbers[i];
                    return true;
                }
                swap(numbers[i], numbers[numbers[i]]);
            }
        }
        return false;
    }
};

构建乘积数组

题目描述

给定一个数组A[0,1,…,n-1],请构建一个数组B[0,1,…,n-1],其中B中的元素B[i]=A[0]A[1]…A[i-1]A[i+1]…A[n-1]。不能使用除法。

解析

B[i]的值可以看做下图的矩阵中每行的乘积。

下三角用连乘可以很容易求得，先算下三角中的连乘，即先计算出B[i]中的一部分，然后将上三角中的数也乘进去。这样一来就只需要两个循环就可以解决这个问题。时间复杂度是O(n);

其实你只需要知道这个是形成一个矩阵，然后每一行是用来计算B[i],每一行的内容则是A[0]到A[n-1]。利用上三角和下三角进行计算。

代码

class Solution {
public:
    vector<int> multiply(const vector<int>& A) {
        vector<int>B(A.size(), 1);
        int tmp = 1;
        for(int i = 0; i < A.size() - 1; ++i){
            tmp *= A[i];
            B[i + 1] *= tmp;
        }
        tmp = 1;
        for(int i = A.size() - 1; i > 0; --i){
            tmp *= A[i];
            B[i - 1] *= tmp;
        }
        return B;
    }
};

正则表达式匹配

题目描述

请实现一个函数用来匹配包括’.’和’‘的正则表达式。模式中的字符’.’表示任意一个字符，而’‘表示它前面的字符可以出现任意次（包含0次）。 在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串”aaa”与模式”a.a”和”abaca”匹配，但是与”aa.a”和”ab*a”均不匹配

解析

“.”按任意字符匹配。如果模式串遇到*字符则有两种状态，第一匹配字符，则字符串后移一位，模式串不变，第二，模式串后移俩位和字符串后移一位，第三，忽略星号。

代码

class Solution {
public:
    bool match(char* str, char* pattern){
        if(str[0] == 0 && pattern[0] == 0){
            return true;
        }else if(pattern[0] && pattern[1] == '*' && match(str, pattern + 2)){
                return true;
        }else if(str[0] && pattern[0] == '.' || str[0] == pattern[0]){
            if(match(str + 1, pattern + 1)){
                return true;
            }else if(pattern[1] == '*' && match(str + 1, pattern)){
                return true;
            }
        }
        return false;
    }
};

表示数值的字符串

题目描述

请实现一个函数用来判断字符串是否表示数值（包括整数和小数）。例如，字符串”+100”,”5e2”,”-123”,”3.1416”和”-1E-16”都表示数值。 但是”12e”,”1a3.14”,”1.2.3”,”+-5”和”12e+4.3”都不是。

解析

暴力

代码

class Solution {
public:
    bool isNumeric(char* string)
    {
        int len = strlen(string);
        int cur = 0;
        bool a = false, b = false, c = false, ans = true;
        while(string[cur] == ' '){
            ++cur;
        }
        for(; cur < len; ++cur){
            if(string[cur] >= '0' && string[cur] <= '9'){
                ans = true;
                a = true;
            }else if(string[cur] == '+' || string[cur] == '-'){
                if(a){
                    return false;
                }else{
                    a = true;
                }
            }else if(string[cur] == 'e' || string[cur] == 'E'){
                if(b){
                    return false;
                }else{
                    b = true;
                    a = false;
                    ans = false;
                }
            }else if(string[cur] == '.'){
                if(c || b){
                    return false;
                }else{
                    c = true;
                    ans = false;
                }
            }else{
                return false;
            }
        }
        return ans;
    }
};

字符流中第一个不重复的字符

题目描述

请实现一个函数用来找出字符流中第一个只出现一次的字符。例如，当从字符流中只读出前两个字符”go”时，第一个只出现一次的字符是”g”。当从该字符流中读出前六个字符“google”时，第一个只出现一次的字符是”l”。

输出描述:

如果当前字符流没有存在出现一次的字符，返回#字符。

解析

哈希表。

代码

class Solution
{
public:
  //Insert one char from stringstream
    Solution():cur(0){}
    void Insert(char ch)
    {
        str += ch;
        ++mp[ch];
        while(cur < str.size() && mp[str[cur]] > 1){
            ++cur;
        }
    }
  //return the first appearence once char in current stringstream
    char FirstAppearingOnce()
    {
        if(cur >= str.size()){
            return '#';
        }
        return str[cur];
    }
private:
    map<char, int>mp;
    string str;
    int cur;
};

链表中环的入口结点

题目描述

给一个链表，若其中包含环，请找出该链表的环的入口结点，否则，输出null。

解析

转：a、第一步，找环中相汇点。分别用fast，slow指向链表头部，slow每次走一步，fast每次走二步，直到fast==slow找到在环中的相汇点。

b、第二步，找环的入口。接上步，当fast==slow时，fast所经过节点数为2x,slow所经过节点数为x,设环中有n个节点，fast比slow多走r圈有2x=rn+x; x=rn;（r为圈数，n为一圈的结点数）

可以看出slow实际走了多个环的步数，再让fast指向链表头部，slow位置不变。

假设链表开头到环接口的距离是y，那么x-y表示slow指针走过的除链表开头y在环中走过的距离，那么slow再走y步，此时fast结点与slow结点相遇，fast == slow ，x-y+y=x = rn，即此时slow指向环的入口。

代码

/*
struct ListNode {
    int val;
    struct ListNode *next;
    ListNode(int x) :
        val(x), next(NULL) {
    }
};
*/
class Solution {
public:
    ListNode* EntryNodeOfLoop(ListNode* pHead)
    {
        ListNode* pFast = pHead;
        ListNode* pSlow = pHead;
        do{
            if(pSlow && pSlow->next){
                pSlow = pSlow->next;
            }else{
                return NULL;
            }
            if(pFast && pFast->next && pFast->next->next){
                pFast = pFast->next->next;
            }else{
                return NULL;
            }
        }while(pFast != pSlow);
        pFast = pHead;
        while(pFast != pSlow){
            pFast = pFast->next;
            pSlow = pSlow->next;
        }
        return pSlow;
    }
};

删除链表中重复的结点

题目描述

在一个排序的链表中，存在重复的结点，请删除该链表中重复的结点，重复的结点不保留，返回链表头指针。 例如，链表1->2->3->3->4->4->5 处理后为 1->2->5

解析

不多说了，因为是排序的链表。

代码

/*
struct ListNode {
    int val;
    struct ListNode *next;
    ListNode(int x) :
        val(x), next(NULL) {
    }
};
*/
class Solution {
public:
    ListNode* deleteDuplication(ListNode* pHead)
    {
		if (pHead == NULL) {
			return NULL;
		}
		ListNode* preNode = NULL;
		ListNode* node = pHead;
		while (node != NULL) {
			if (node->next != NULL && node->val == node->next->val) {
				int value = node->val;
				while (node->next != NULL && node->next->val == value) {
					node = node->next;
				}
				if (preNode == NULL) {
					pHead = node->next;
				} else {
					preNode->next = node->next;
				}
			} else {
				preNode = node;
			}
            node = node->next;
		}
		return pHead;
    }
};

二叉树的下一个结点

题目描述

给定一个二叉树和其中的一个结点，请找出中序遍历顺序的下一个结点并且返回。注意，树中的结点不仅包含左右子结点，同时包含指向父结点的指针。

解析

我们可发现分成两大类：1、有右子树的，那么下个结点就是右子树最左边的点；（eg：D，B，E，A，C，G） 2、没有右子树的，也可以分成两类，a)是父节点左孩子（eg：N，I，L） ，那么父节点就是下一个节点 ； b)是父节点的右孩子（eg：H，J，K，M）找他的父节点的父节点的父节点…直到当前结点是其父节点的左孩子位置。如果没有eg：M，那么他就是尾节点。

代码

/*
struct TreeLinkNode {
    int val;
    struct TreeLinkNode *left;
    struct TreeLinkNode *right;
    struct TreeLinkNode *next;
    TreeLinkNode(int x) :val(x), left(NULL), right(NULL), next(NULL) {
        
    }
};
*/
class Solution {
public:
    TreeLinkNode* GetNext(TreeLinkNode* pNode)
    {
        if(pNode == NULL){
            return pNode;
        }
        if(pNode->right){
            TreeLinkNode* p = pNode->right;
            while(p->left){
                p = p->left;
            }
            return p;
        }
        else{
            TreeLinkNode* p = pNode->next;
            while(p && p->right == pNode){
                pNode = p;
                p = p->next;
            }
            return p;
        }
        return NULL;
    }
};

对称的二叉树

题目描述

请实现一个函数，用来判断一颗二叉树是不是对称的。注意，如果一个二叉树同此二叉树的镜像是同样的，定义其为对称的。

解析

【分析1】首先我们需要明确一下镜像二叉树的概念，简单来说就是左子树与右子树对调。而根据树的递归定义可以，左子树和右子树的定义也是递归而言的。

【分析2】接下来我们需要明确两棵二叉树什么时候相同。显然，根结点的值相等，左右子树相同，则这两颗二叉树相同。显然，在判断两棵二叉树是否相同时也需要递归地进行判断。

【分析3】题目中并不是想让我们判断任意两棵二叉树是否相同，而是要求我们判断一棵二叉树和它的镜像二叉树是否相同。因此我们判断相同的条件不就很明显的变成了：根结点对应的值相等，原二叉树Root的左子树与其镜像二叉树Root’的右子树相同，且原二叉树Root的右子树与其镜像二叉树Root’的左子树相同。如此递归下去。直到① 如果Root和Root’均为空，则返回true；② 如果Root为空或者Root’为空，则返回false；③ 如果Root对应的值与Root’对应的值不相等，则返回false。

代码

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};
*/
class Solution {
public:
    bool check(TreeNode* pRoot_1, TreeNode* pRoot_2){
        return pRoot_1->val == pRoot_2->val;
    }
    bool isSymmetrical(TreeNode* pRoot)
    {
        if(pRoot == NULL){
            return true;
        }
        return dfs(pRoot->left, pRoot->right);
    }
    bool dfs(TreeNode* pRoot_1, TreeNode* pRoot_2){
        if(pRoot_1 == NULL || pRoot_2 == NULL){
            if(pRoot_1 == NULL && pRoot_2 == NULL){
                return true;
            }
            return false;
        }
        if(check(pRoot_1, pRoot_2)){
            if(dfs(pRoot_1->left, pRoot_2->right)){
                return dfs(pRoot_1->right, pRoot_2->left);
            }
        }
        return false;
    }
};

按之字形顺序打印二叉树

题目描述

请实现一个函数按照之字形打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右至左的顺序打印，第三行按照从左到右的顺序打印，其他行以此类推。

解析

广度优先遍历。两个栈代替队列储存数据。

代码

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};
*/
class Solution {
public:
    vector<vector<int> > Print(TreeNode* pRoot) {
        stack<TreeNode*>que;
        stack<TreeNode*>stk;
        vector<vector<int> >vv;
        if(!pRoot){
            return vv;
        }
        que.push(pRoot);
        while(!que.empty() || !stk.empty()){
            vector<int>v;
            if(!que.empty()){
                while(!que.empty()){
                    TreeNode* tmp = que.top();
                    que.pop();
                    v.push_back(tmp->val);
                    if(tmp->left){
                        stk.push(tmp->left);
                    }
                    if(tmp->right){
                        stk.push(tmp->right);
                    }
                }
            }
            else{
                while(!stk.empty()){
                    TreeNode* tmp = stk.top();
                    stk.pop();
                    v.push_back(tmp->val);
                    if(tmp->right){
                        que.push(tmp->right);
                    }
                    if(tmp->left){
                        que.push(tmp->left);
                    }
                }
            }
            vv.push_back(v);
        }
        return vv;
    }
};

把二叉树打印成多行

题目描述

从上到下按层打印二叉树，同一层结点从左至右输出。每一层输出一行。

解析

带属性的广度优先遍历。

代码

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};
*/
class Solution {
public:
    vector<vector<int> > Print(TreeNode* pRoot) {
            vector<vector<int> > vv;
            vector<int> ve;
            queue<TreeNode*> que;
            queue<int> dque;
            int depth=0;
            que.push(pRoot);
            dque.push(depth);
            TreeNode *node;
            while(!que.empty()){
                node=que.front();
                if(depth!=dque.front()){
                    vv.push_back(ve);
                    ve.clear();
                    depth=dque.front();
                }
                que.pop();
                dque.pop();
                if(node){
                    que.push(node->left);
                    que.push(node->right);
                    dque.push(depth+1);
                    dque.push(depth+1);
                    ve.push_back(node->val);
                }
            }
            return vv;
        
    }
};

序列化二叉树

题目描述

请实现两个函数，分别用来序列化和反序列化二叉树

解析

二叉树的序列化是指：把一棵二叉树按照某种遍历方式的结果以某种格式保存为字符串，从而使得内存中建立起来的二叉树可以持久保存。

序列化可以基于 先序、中序、后序、按层 的二叉树遍历方式来进行修改。原理都是一样的（即遍历顺序不同而已，对每个结点的处理都是一样的），序列化的结果是一个字符串，序列化时通过 某种符号表示空节点（#），以 ！ 表示一个结点值的结束（value!）。

这里以先序遍历的方式进行序列化举例：

先序序列化二叉树==定义一个stringbuilder保存序列过程中的结果：按照先序遍历方式遍历二叉树，若结点非空则把 “结点值!” append到builder中；若结点空则把 “#!” append到builder中；最后用builder生成字符串就是序列化结果。

代码

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};
*/
class Solution {
public:
    char* Serialize(TreeNode *root) {
        string str;
        if(root){
            str = to_string(root->val);
            str = str + "," + Serialize(root->left);
            str = str + "," + Serialize(root->right);
        }else{
            str = "#";
        }
        char* ret = new char[str.size()];
        strcpy(ret,str.c_str());
        return ret;
    }
    TreeNode* dfs(char * &str) {
        if(*str == ','){
            ++str;
        }
        if(str){
            TreeNode* Tree = new TreeNode(0);
            if(str && *str >= '0' && *str <= '9'){
                while(*str >= '0' && *str <= '9'){
                    Tree->val *= 10;
                    Tree->val += *str - '0';
                    ++str;
                }
                Tree->left = dfs(str);
                Tree->right = dfs(str);
                return Tree;
            }else if(*str == '#'){
                ++str;
                return NULL;
            }
        }
        return NULL;
    }
    TreeNode* Deserialize(char * str){
        return dfs(str);
    }
};

二叉搜索树的第k个结点

题目描述

给定一棵二叉搜索树，请找出其中的第k小的结点。例如， （5，3，7，2，4，6，8） 中，按结点数值大小顺序第三小结点的值为4。

解析

搜索树按从小到大的顺序排列正好就是中序遍历； 所以按照中序遍历查找，第k个节点就是结果。

代码

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};
*/
class Solution {
public:
    int cnt;
    TreeNode* KthNode(TreeNode* pRoot, int k)
    {
        cnt = 0;
        return dfs(pRoot, k);
    }
    TreeNode* dfs(TreeNode* pRoot, int k){
        if(pRoot == NULL){
            return NULL;
        }
        if(pRoot->left){
            TreeNode* tmp = dfs(pRoot->left, k);
            if(tmp){
                return tmp;
            }
        }
        ++cnt;
        if(cnt == k){
            return pRoot;
        }
        if(pRoot->right){
            TreeNode* tmp = dfs(pRoot->right, k);
            if(tmp){
                return tmp;
            }
        }
        return NULL;
    }
};

数据流中的中位数

题目描述

如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。我们使用Insert()方法读取数据流，使用GetMedian()方法获取当前读取数据的中位数。

解析

最大堆和最小堆结合。最大堆储存前n/2个数，最小堆储存后n/2个数。偶数个数据，那么中位数可以由大小堆堆顶的数得到，如果数据的数目是奇数，那么输出最大堆堆顶。

代码

class Solution {
public:
    void Insert(int num)
    {
        if(max_que.size() == min_que.size()){
            if(max_que.empty() || max_que.top() >= num || min_que.top() >= num){
                max_que.push(num);
            }else{
                max_que.push(min_que.top());
                min_que.pop();
                min_que.push(num);
            }
        }else{
            if(max_que.top() >= num){
                min_que.push(max_que.top());
                max_que.pop();
                max_que.push(num);
            }else{
                min_que.push(num);
            }
        }
    }

    double GetMedian()
    { 
        if(max_que.size() == min_que.size()){
            return (min_que.top() + max_que.top()) / 2.0;
        }else{
            return max_que.top();
        }
    }
private:
    priority_queue<int, vector<int>, greater<int> >min_que;
    priority_queue<int>max_que;
};

滑动窗口的最大值

题目描述

给定一个数组和滑动窗口的大小，找出所有滑动窗口里数值的最大值。例如，如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3，那么一共存在6个滑动窗口，他们的最大值分别为{4,4,6,6,6,5}； 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个： {[2,3,4],2,6,2,5,1}， {2,[3,4,2],6,2,5,1}， {2,3,[4,2,6],2,5,1}， {2,3,4,[2,6,2],5,1}， {2,3,4,2,[6,2,5],1}， {2,3,4,2,6,[2,5,1]}。

解析

我们可以用STL中的deque，以数组{2,3,4,2,6,2,5,1}为例，来细说整体思路。

数组的第一个数字是2，把它存入队列中。第二个数字是3，比2大，所以2不可能是滑动窗口中的最大值，因此把2从队列里删除，再把3存入队列中。第三个数字是4，比3大，同样的删3存4。此时滑动窗口中已经有3个数字，而它的最大值4位于队列的头部。

第四个数字2比4小，但是当4滑出之后它还是有可能成为最大值的，所以我们把2存入队列的尾部。下一个数字是6，比4和2都大，删4和2，存6。就这样依次进行，最大值永远位于队列的头部。

但是我们怎样判断滑动窗口是否包括一个数字？应该在队列里存入数字在数组里的下标，而不是数值。当一个数字的下标与当前处理的数字的下标之差大于或者相等于滑动窗口大小时，这个数字已经从窗口中滑出，可以从队列中删除。

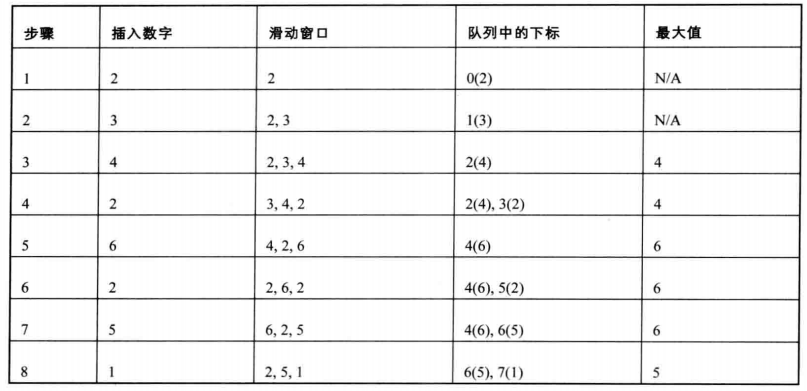
代码

class Solution {
public:
    vector<int> maxInWindows(const vector<int>& num, unsigned int size){
        deque<int>dq, vis;
        vector<int>v;
        for(unsigned int i = 0; i < num.size(); ++i){
            if(!vis.empty() && i - vis.front() >= size){
                dq.pop_front();
                vis.pop_front();
            }
            while(!dq.empty() && dq.back() <= num[i]){
                    dq.pop_back();
                    vis.pop_back();
            }
            dq.push_back(num[i]);
            vis.push_back(i);
            if(i >= size - 1){
                v.push_back(dq.front());
            }
        }
        return v;
    }
};

矩阵中的路径

题目描述

请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向左，向右，向上，向下移动一个格子。如果一条路径经过了矩阵中的某一个格子，则之后不能再次进入这个格子。 例如 a b c e s f c s a d e e 这样的3 X 4 矩阵中包含一条字符串”bcced”的路径，但是矩阵中不包含”abcb”路径，因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后，路径不能再次进入该格子。

解析

dfs(回溯)。创建一个状态数组对访问的字符进行标记。首先，遍历这个矩阵，如果矩阵中某字符和目标字符首字母相等，则以该字符为起点dfs深搜，否则继续遍历。一直重复这个过程，直到路径字符串上所有字符都在矩阵中找到格式的位置。

代码

class Solution {
public:
    bool dfs(char* matrix, int x, int y, char* str, int cur, int rows, int cols){
        if(x < 0 || y < 0 || x >= rows || y >= cols || vis[x * cols + y] == true || str[cur] != matrix[x * cols + y]){
            return false;
        }
        vis[x * cols + y] = true;
        if(cur >= len - 1){
            return true;
        }
        for(int i = 0; i < 4; ++i){
            if(dfs(matrix, x + road[i][0], y + road[i][1], str, cur + 1, rows, cols) == true){
                return true;
            }
        }
        vis[x * cols + y] = false;
        return false;
    }
    bool hasPath(char* matrix, int rows, int cols, char* str){
        if(matrix[0] == 0){
            return false;
        }
        len = strlen(str);
        vis.resize(cols * rows, false);
        for(int i = 0; i < rows; ++i){
            for(int j = 0; j < cols; ++j){
                if(matrix[i* cols + j] == str[0]){
                    if(dfs(matrix, i, j, str, 0, rows, cols) == true){
                        return true;
                    }
                }
            }
        }
        return false;
    }
private:
    int len;
    vector<bool>vis;
    int road[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
};

机器人的运动范围

题目描述

地上有一个m行和n列的方格。一个机器人从坐标0,0的格子开始移动，每一次只能向左，右，上，下四个方向移动一格，但是不能进入行坐标和列坐标的数位之和大于k的格子。 例如，当k为18时，机器人能够进入方格（35,37），因为3+5+3+7 = 18。但是，它不能进入方格（35,38），因为3+5+3+8 = 19。请问该机器人能够达到多少个格子？

解析

dfs(回溯)。创建一个状态数组对访问的格子进行标记，但是这里需要计算所有能够走的格子总数，实际上只需要对下一个进行访问的格子进行计算，进行从上、下、左、右四个方向进行递归，就可以计算出可以达到的格子总数了。

代码

class Solution {
public:
    int movingCount(int threshold, int rows, int cols){
        vis.resize(rows * cols, false);
        return dfs(threshold, rows, cols, 0, 0);
    }
private:
    int dfs(int threshold, int rows, int cols, int x, int y){
        if(x < 0 || y < 0 || x >= rows || y >= cols || vis[x * cols + y] || threshold < check(x) + check(y)){
            return 0;
        }
        vis[x * cols + y] = true;
        int ans = 1;
        for(int i = 0; i < 4; ++i){
            ans += dfs(threshold, rows, cols, x + road[i][0], y + road[i][1]);
        }
        return ans;
    }
    int check(int num){
        int res = 0;
        while(num){
            res += num % 10;
            num /= 10;
        }
        return res;
    }
    vector<bool>vis;
    int road[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
};