[图论]二分图匹配基本算法之匈牙利算法解析

二分图概念

二分图（二部图），图论一种特殊的模型。设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（ i，j ）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。

简而言之，一个图所有的顶点被分成两部分，同一部分的顶点之间没有边。如图所示：

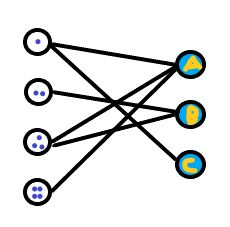
二分图匹配

给定一个二分图G，在G的一个子图M中，M的边集{E}中的任意两条边都不依附于同一个顶点，则称M是一个匹配。
极大匹配(Maximal Matching)是指在当前已完成的匹配下,无法再通过增加未完成匹配的边的方式来增加匹配的边数。最大匹配(maximum matching)是所有极大匹配当中边数最大的一个匹配。选择这样的边数最大的子集称为图的最大匹配问题。
如果一个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完全匹配，也称作完备匹配。

增广路经

增广路径的定义：设M为二分图G已匹配边的集合，若P是图G中一条连通两个未匹配顶点的路径（P的起点在X部，终点在Y部，反之亦可），并且属M的边和不属M的边(即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广路径。
增广路径是一条“交错轨”。也就是说, 它的第一条边是目前还没有参与匹配的,第二条边参与了匹配,第三条边没有..最后一条边没有参与匹配,并且起点和终点还没有被选择过，这样交错进行,显然P有奇数条边

由增广路的定义可以推出下述三个结论：

P的路径长度必定为奇数，第一条边和最后一条边都不属于M，因为两个端点分属两个集合，且未匹配。
P经过取反操作可以得到一个更大的匹配M’。
M为G的最大匹配当且仅当不存在相对于M的增广路径。

匈牙利算法

匈牙利算法是基于Hall定理中充分性证明的思想，它是部图匹配最常见的算法，该算法的核心就是寻找增广路径，它是一种用增广路径求二分图最大匹配的算法。

匈牙利算法基本模式：

初始时最大匹配为空

while 找到增广路经

do 把增广路径加入到最大匹配中去

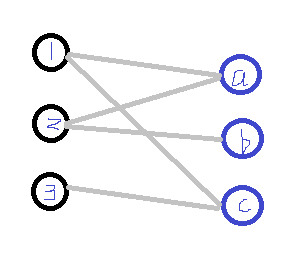
具体过程如图所示：

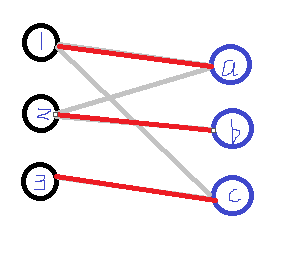
1.如图所示，1可以与a，c匹配，2可以与a，b匹配，3可以与c匹配

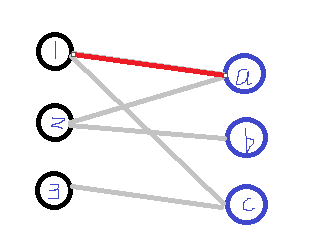
2.首先将对1进行搜索，1可以与a匹配，则将1与a相连

3.再对2进行搜索，2可以与a匹配

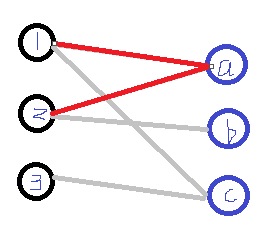
4.但是a已经与1匹配了，那么顺着a->1这条路找到1，再对1进行搜索，发现1还可以与c进行匹配，并且当前c还未与任何X区顶点匹配，则将1与c相连

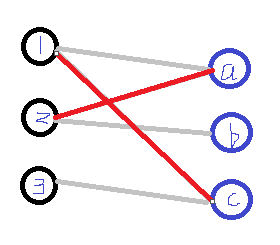
5.现在对3进行匹配，发现3可以与c匹配

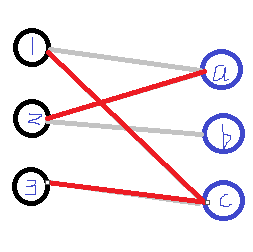
6.这时发现c已经匹配了，则顺着c->1这条路找到1，再对1进行搜索，发现1还可以与a匹配

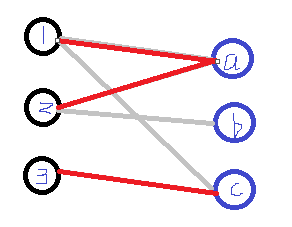
7.但a也已经匹配了，则顺着a->2这条路找到2，这时发现2还可以与b匹配，并且b当前还未与任何X顶点匹配，则将2与b匹配，之后得到的结果即为最大匹配

以下是实现代码

bool find(int x) {	//寻找增广路
	for (int i = 1; i <= N; i++) {	//遍历Y部分顶点
		if (road[x][i] && !vis[i]) {	//Y某顶点与X有路且未标记
			vis[i] = true;
			if (!link[i] || find(link[i])) {	//如果Y顶点当前未与其他X匹配则直接与该点匹配，否则寻找增广路，然后将Y顶点与该顶点匹配
				link[i] = x;
				return true;
			}
		}
	}
	return false;
}

主程序调用：

for(int i = 1; i <= N; i++){	//对每一个X部分顶点进行遍历
  memset(vis,false,sizeof(vis));
  if(find(i)){	//寻找增光路
    ans++;	//最大匹配数量加1
  }
}

例题：POJ3041

给一个N*N的矩阵，有些格子有障碍，要求我们消除这些障碍，问每次消除一行或一列的障碍，

最少要几次。这里将每行x看成一个X结点，每列Y看成一个Y结点，障碍的坐标x,y看成X到Y的

一条边，构建出图后，就变成了找最少的点，使得这些点与所有的边相邻，即最小点覆盖问题。

又继续敲了一遍匈牙利算法

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
int N, K, ans;
int road[520][520], head[520];
bool vis[520];
bool find(int x) {
	for (int i = 1; i <= N; i++) {
		if (road[x][i] && !vis[i]) {
			vis[i] = true;
			if (!head[i] || find(head[i])) {
				head[i] = x;
				return true;
			}
		}
	}
	return false;
}
int main() {
	while (cin >> N >> K) {
		ans = 0;
		int x, y;
		memset(road, 0, sizeof(road));
		memset(head, 0, sizeof(head));
		for (int i = 1; i <= K; i++)
		{
			cin >> x >> y;
			road[x][y] = 1;
		}
		for (int i = 1; i <= N; i++) {
			memset(vis, false, sizeof(vis));
			if (find(i)) {
				ans++;
			}
		}
		cout << ans << endl;
	}
	return 0;
}