- 语法分析
- 自顶向下语法分析
- 确定分析
- 不确定分析
- 自底向上语法分析
- 算符优先分析
- LR分析
- 自顶向下语法分析
自顶向下语法分析
确定分析(LL(1)文法)
例1:
G[S]:
S -> pA | qB
A -> cAd | a
B -> dB | b
W = pccadd。
推导过程如下:S => pA => pcAd => pccAdd => pccadd。
- S S S S
/ \ / \ / \ / \
p A => p A => p A => p A
c A d c A d c A d/ | \ / | \ / | \
c A d c A d/ | \ / | \
|a
例2:
G[S]:
S->Ap
S->Bq
A->a
A->cA
B->b
B->dB
W = ccap,推导过程:
S => aP => cAp => ccAp => ccap。
FIRST(a)
a的开始符号集或首符号集。
例2:FIRST(Ap) = {a, c}。
FIRST(Bq) = {b, d}。
FIRST(S) = {a, b, c, d}。
###FOLLOW(A)
若Aa,a ∈ FOLLOW(A)。若a = ε,则# ∈ FOLLOW(A)。
SELECT(A->a)
a不为ε,则SELECT(A->a) = FIRST(a)。
否则,SELECT(A->a) = FIRST(a) - ε + FOLLOW(A)。
LL(1)
定义:
第1个L表示从左往右扫描字符串。
第2个L表示采用最左推导。
1表示只需向右看1个字符即可选择哪个产生式。(为了提高效率,最多为2)。
充要条件:
SELLECT(A->a) ∩ SELECT(A->b) = 空集。(a,b不能同时能ε)。
通俗理解就是a和b不能有相同前缀。
LL(1)文法判别步骤
求出能推出 ε 的非终结符。(未定,是,否)
计算FIRST集
计算FOLLOW集
计算SELECT集
方法
递归子程序法
对应文法中每个非终结符编写一个递归过程,每个过程的功能是识别由非终结符推出的串,当某非终结符的产生式有多个候选时能够按LL(1)形式可唯一确定地选择某个候选进行推导。
当文法满足LL(1)条件时,构造不带回溯的自上而下分析程序。
该分析程序由一组递归过程组成,每个过程对应文法的一个非终结符。
注意
不是所有的aij的first集的交集都为空,仅针对一个VN的候选式有如此的约定。
预测分析法
特征 :
根据当前输入符号,为当前要处理的非终结符选择产生式。
表驱动的预测分析器包含:
- 一个输入缓冲区
- 一个栈
- 一张分析表
- 一个输出流
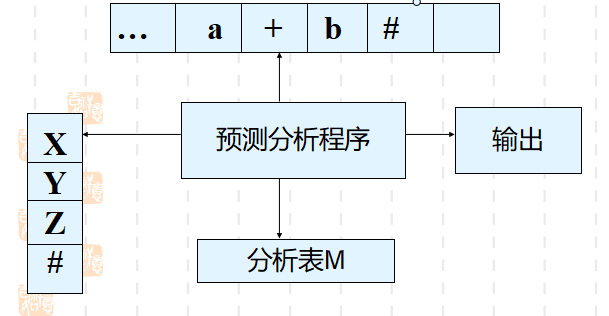
预测分析表M
预测分析表是一个M[A,a]形式的矩阵。
其中: A为非终结符,a为终结符或#。
M[A,a]中存放着一条关于A的产生式,指出当A面临a时所应采取的候选;
M[A,a]中也可能存放一条“出错标志”,指出A不应该面临a。
例:对于文法G
- E→TE’
- E’ → +TE’|ε
- T →FT’
- T’→*FT’| ε
- F→(E)|id
其预测分析表为:
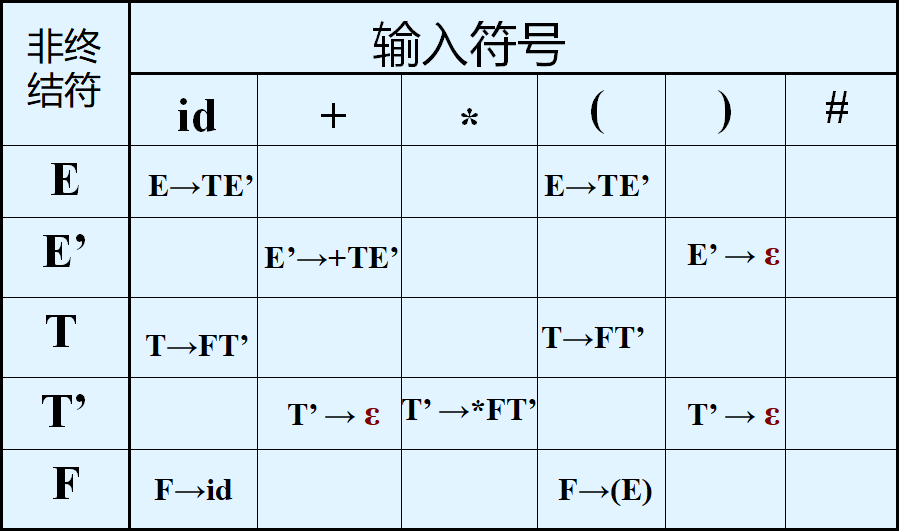
解:
1 | FIRST(E)={ (, id } |
预测分析器
预测分析程序的算法:
输入:串w和文法G的分析表M
输出:如果w属于L(G),则输出w的最左推导,否则报错
方法:开始时,#S在栈里,w#在输入缓冲区
令ip指向w #的第一个符号,令X是栈顶符号,a是ip指向的符号
预测分析器的工作方式:当前栈顶符号X和当前输入符号为a,则语法分析器的动作为:
- 如果X=a≠#,则POP,advance
- 如果X ∈VN,查M[X,a]表,若M[X,a]=X→UVW,则用WVU替换栈顶;若M[X,a]=error,则调用错误恢复程序。
- 如果X=a=#,分析成功。
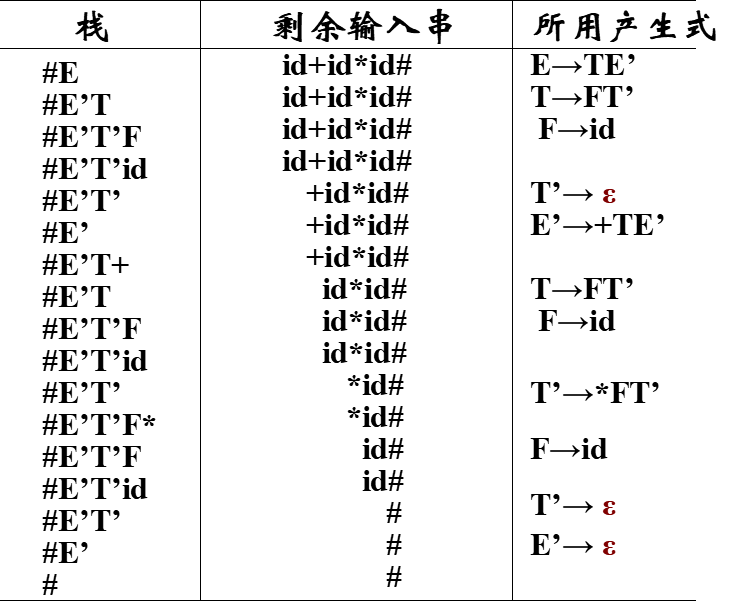
句子id+id*id的分析过程:
不确定分析(简)
原理:
匹配,匹配不了回溯继续匹配,直到全部匹配不了或匹配成功为止。(非常暴力)
由于相同左部的产生式的右部FIRST集交集不为空而引起回溯。
S->xAy
S->ab|a
由于相同左部非终结符的右部可为 ε ,且非终结符的FOLLOW集中含有其他产生式右部FIRST集的元素。
S->aAS
S->b
A->bAS
A->ε
由于文法含有左递归。
S->Sa
S->b
部分不确定分析转确定分析
左递归消除
直接左递归消除
采用下列变换公式消除直接左递归,把直接左递归改写为右递归。
如:G[S]: S→Sa | b
可改写为:
S→bS’
S’→aS’|ε
改写后的文法所描述的L(G)={ba^n| n>=0}
一般而言,假定关于P的全部产生式是
P→Pa1 | Pa2 | … | Pam | b1 | b2|…|bn 其中,每个a都不等于ε,而每个都不以P开头,那么,消除P的直接左递归性就是改写这些规则:
P→b1P’ | b2P’ | … | bnP’
P’→a1P’ | a2P’ |… | amP’ | ε
间接左递归消除
间接左递归的消除需先将间接左递归变为直接左递归,然后再按第1种方法消除直接左递归。
代入法
将一个产生式规则右部的a中的Vn N替换为N的候选式。如果N有n个候选式,右边a重复n次,而且每一次重复都有N的不同候选式来代替N。
例如:N →a | Bc | ε 在S→Nq中的代入结果S→aq | Bcq | q。
回溯消除
回溯产生的根源:头字符集合的问题。例如A->ab|a。
提取公因子
经过反复提取左因子,就能够把每个非终结符(包括新引进者)的所有候选首符集变成为两两不相交。
例:考察文法G[S]:
S → iCtS | iCtSeS | aC → b
解:由于S的前两个候选项中含有左因子iCtS,提取左因子之后,等价文法G’如下:
S → iCtSS’ | a
S’ →eS |ε
C → b

